概率分佈
用以表述隨機變數取值的概率規律
概率分佈,是指用於表述隨機變數取值的概率規律。事件的概率表示了一次試驗中某一個結果發生的可能性大小。若要全面了解試驗,則必須知道試驗的全部可能結果及各種可能結果發生的概率,即隨機試驗的概率分佈。如果試驗結果用變數X的取值來表示,則隨機試驗的概率分佈就是隨機變數的概率分佈,即隨機變數的可能取值及取得對應值的概率。根據隨機變數所屬類型的不同,概率分佈取不同的表現形式。
概率分佈律[law of probability distribution]簡稱概率律或概率分佈。上描述隨機變數取值規律的概率測度。假定 是概率空間 上的隨機變數則由
所定義的 上的集函數 F 是一個概率測度,稱為隨機交量 的概率分佈律。對於任何 隨機變數 落入B中的概率可通過計算B 的測度F(B) 得出這就是說概率分佈F 完全刻畫了 取值的概率規律。
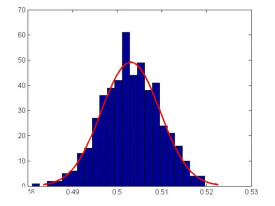
正態分佈是一種很重要的連續型隨機變數的概率分佈。生物現象中有許多變數是服從或近似服從正態分佈的,如家畜的體長、體重、產奶量、產毛量、血紅蛋白含量、血糖含量等。許多統計分析方法都是以正態分佈為基礎的。此外,還有不少隨機變數的概率分佈在一定條件下以正態分佈為其極限分佈。因此在統計學中,正態分佈無論在理論研究上還是實際應用中,均佔有重要的地位。
關於正態分佈的概率計算,我們先從標準正態分佈著手。這是因為,一方面標準正態分佈在正態分佈中形式最簡單,而且任意正態分佈都可化為標準正態分佈來計算;另一方面,人們已經根據標準正態分佈的分佈函數編製成正態分佈表以供直接查用。