拉格朗日量

1788年，約瑟夫·拉格朗日建立拉格朗日力學，是對經典力學的一種的新的理論表述，著重於數學解析的方法，是分析力學的重要組成部分。它有一個基本假設是具有 n 個自由度的系統，其運動狀態完全由 n 個廣義坐標及廣義速度決定。力學系統的運動狀態由一個廣義坐標和廣義速度的函數描述：此函數即拉格朗日量（函數）。 

約瑟夫·拉格朗日

約瑟夫·路易斯·拉格朗日（Joseph-Louis Lagrange 1735~1813）

法國數學家、物理學家。1736年1月25日生於義大利都靈，1813年4月10日卒於巴黎。他在數學、力學和天文學三個學科領域中都有歷史性的貢獻，其中尤以數學方面的成就最為突出。

拉格朗日生平

拉格朗日1736年1月25日生於義大利西北部的都靈。父親是法國陸軍騎兵里的一名軍官，後由於經商破產，家道中落。據拉格朗日本人回憶，如果幼年是家境富裕，他也就不會作數學研究了，因為父親一心想把他培養成為一名律師。拉格朗日個人卻對法律毫無興趣。

到了青年時代，在數學家雷維里的教導下，拉格朗日喜愛上了幾何學。17歲時，他讀了英國天文學家哈雷的介紹牛頓微積分成就的短文《論分析方法的優點》后，感覺到“分析才是自己最熱愛的學科”，從此他迷上了數學分析，開始專攻當時迅速發展的數學分析。

18歲時，拉格朗日用義大利語寫了第一篇論文，是用牛頓二項式定理處理兩函數乘積的高階微商，他又將論文用拉丁語寫出寄給了當時在柏林科學院任職的數學家歐拉。不久后，他獲知這一成果早在半個世紀前就被萊布尼茲取得了。這個並不幸運的開端並未使拉格朗日灰心，相反，更堅定了他投身數學分析領域的信心。

中年時的約瑟夫·拉格朗日1755年拉格朗日19歲時，在探討數學難題“等周問題”的過程中，他以歐拉的思路和結果為依據，用純分析的方法求變分極值。第一篇論文“極大和極小的方法研究”，發展了歐拉所開創的變分法，為變分法奠定了理論基礎，變分法的創立，使拉格朗日在都靈聲名大震，並使他在19歲時就當上了都靈皇家炮兵學校的教授，成為當時歐洲公認的第一流數學家。1756年，受歐拉的舉薦，拉格朗日被任命為普魯士科學院通訊院士。

1764年，法國科學院懸賞徵文，要求用萬有引力解釋月球天平動問題，他的研究獲獎。接著又成功地運用微分方程理論和近似解法研究了科學院提出的一個複雜的六體問題(木星的四個衛星的運動問題)，為此又一次於1766年獲獎。

1766年德國的腓特烈大帝向拉格朗日發出邀請時說，在“歐洲最大的王”的宮廷中應有“歐洲最大的數學家”。於是他應邀前往柏林，任普魯士科學院數學部主任，居住達20年之久，開始了他一生科學研究的鼎盛時期。在此期間，他完成了《分析力學》一書，這是牛頓之後的一部重要的經典力學著作。書中運用變分原理和分析的方法，建立起完整和諧的力學體系，使力學分析化了。他在序言中宣稱：力學已經成為分析的一個分支。

1783年，拉格朗日的故鄉建立了"都靈科學院"，他被任命為名譽院長。1786年腓特烈大帝去世以後，他接受了法王路易十六的邀請，離開柏林，定居巴黎，直至去世。

這期間他參加了巴黎科學院成立的研究法國度量衡統一問題的委員會，並出任法國米制委員會主任。1799年，法國完成統一度量衡工作，制定了被世界公認的長度、面積、體積、質量的單位，拉格朗日為此做出了巨大的努力。

1791年，拉格朗日被選為英國皇家學會會員，又先後在巴黎高等師範學院和巴黎綜合工科學校任數學教授。1795年建立了法國最高學術機構——法蘭西研究院后，拉格朗日被選為科學院數理委員會主席。此後，他才重新進行研究工作，編寫了一批重要著作：《論任意階數值方程的解法》、《解析函數論》和《函數計算講義》，總結了那一時期的特別是他自己的一系列研究工作。

1813年4月3日，拿破崙授予他帝國大十字勳章，但此時的拉格朗日已卧床不起，4月11日早晨，拉格朗日逝世。

5個拉格朗日點的情況

L1

在M1和M2兩個大天體的連線上，且在它們之間。

例如：一個圍繞太陽旋轉的物體，它距太陽的距離越近，它的軌道周期就越短。但是這忽略了地球的萬有引力對其產生的拉力的影響。如果這個物體在地球與太陽之間，地球引力的影響會減弱太陽對這物體的拉力，因此增加了這個物體的軌道周期。物體距地球越近，這種影響就越大。在L1點，物體的軌道周期恰好等於地球的軌道周期。太陽及日光層探測儀（SOHO）（NASA關於SOHO工程的網站 ）即圍繞日-地系統的L1點運行。

L2

在兩個大天體的連線上，且在較小的天體一側。

例如：相似的影響發生在地球的另一側。一個物體距太陽的距離越遠，它的軌道周期通常就越長。地球引力對其的拉力減小了物體的軌道周期。在L2點，軌道周期變得與地球的相等。

L2通常用於放置空間天文台。因為L2的物體可以保持背向太陽和地球的方位，易於保護和校準。

威爾金森微波各向異性探測器已經圍繞日-地系統的L2點運行。詹姆斯·韋伯太空望遠鏡將要被放置在日-地系統的L2點上。

L3

在兩個大天體的連線上，且在較大的天體一側。

例如：第三個拉格朗日點，L3，位於太陽的另一側，比地球距太陽略微遠一些。地球與太陽的合拉力再次使物體的運行軌道周期與地球相等。

一些科幻小說和漫畫經常會在L3點描述出一個“反地球” 。

L4

在以兩天體連線為底的等邊三角形的第三個頂點上，且在較小天體圍繞較大天體運行軌道的前方。

L5

在以兩天體連線為底的等邊三角形的第三個頂點上，且在較小天體圍繞較大天體運行軌道的後方。

L4和L5有時稱為“三角拉格朗日點”或“特洛伊點”。

土衛三的L4和L5點有兩個小衛星，土衛十三和土衛十四。土衛四在L4點有一個衛星土衛十二。

拉格朗日量（又稱拉格朗日函數）是動能T 與勢能V 的差值。通常，動能的參數為廣義速度（符號上方的點號表示對於時間t的全導數），而勢能的參數為廣義坐標，所以，拉格朗日量的參數。

假設一個物理系統的拉格朗日量為 ，則此物理系統的運動，以拉格朗日方程表示為

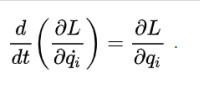
拉格朗日量方法的優點在於，它是一個微擾理論，這個理論不僅包括了樹圖能級貢獻，而且也包含了圈貢獻。目前，這樣的計算只能對結果的數量級進行估計，因為沒有充足的實驗數據去確定拉格朗日量抵消項的任意係數。然而，它們提供了一個圈圖貢獻大小的線索。我們將介紹與此相關的兩個例子：第一個是超精細質量劈裂下圈效應的大小。第二個例子是通過手征的圈效應給出比率，其中fDs和Df 分別為介子和 介子的輕子衰變常數。計算手征圈效應的其它例子還包括對強耦合常數的修正，對半輕子的形狀因子的修正和以及對B介子和 D介子輻射衰變與稀有衰變的修正。 

有效拉格朗日方法最主要的缺陷是在拉格朗日量中有大量的耦合常數。即使在輕介子微商和1Qm展開的最低階，不得不使用數據確定幾個耦合。一個典型的例子是已經提及到的D*Dπ耦合常數，目前確定它的實驗數據仍不充足。在缺少實驗數據的情況下，人們也可以依靠理論研究提供的結果，比如來自 求和規則或勢模型關於它的或者 晶格模擬。另一個可選擇的辦法是不僅通過強相互作用，而且通過介子之間的弱相互作用和電磁相互作用獲取相關信息。事實上，手征拉格朗日量在這些過程中的應用不僅為決定體系的耦合常數提供了可能，而且提供了由對稱聯繫的不同過程之間的定量關係。要做到這一點，通常使用兩種方法：第一種方法是用手征對稱性和重夸克味對稱性聯繫不同弱躍遷和電磁躍遷的振幅之間的關係。第二種方法是利用手征拉格朗日量來計算不同的振幅。無論使用哪種方法，都需要對形狀因子的q²行為做出一些假設。