橢偏儀
光學測量儀器
橢徠偏儀是一種用於探測薄膜厚度、光學常數以及材料微結構的光學測量儀器。由於測量精度高,適用於超薄膜,與樣品非接觸,對樣品沒有破壞且不需要真空,使得橢偏儀成為一種極具吸引力的測量儀器。
橢偏儀1
成像橢圓偏振技術正在引起越來越多的興趣。研究人員發現利用成像橢偏技術可實現超小塊薄膜分析、原位橢偏測量、各種液體環境下的橢偏分析並且可以實現和多種技術聯用,如布魯斯特角顯微鏡、表面等離子共振、原子力顯微鏡、石英晶體微天平、LB槽、反射光譜儀、太赫茲光譜儀以及拉曼光譜儀等等。這些新特點拓展了橢偏儀的應用領域。這橢偏技術帶來了新的研究熱點的同時也給該技術帶來了挑戰,例如在非穩定液體表面的薄膜的測量和顯微成像等。
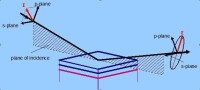
下圖給出了橢偏儀的基本光學物理結構。已知入射光的偏振態,偏振光在樣品表面被反射,測量得到反射光偏振態(幅度和相位),計算或擬合出材料的屬性。
橢偏儀2
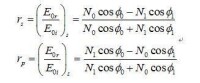
橢偏儀3
橢偏儀4
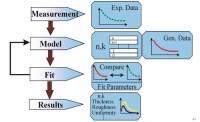
通常橢偏儀測量作為波長和入射角函數的ρ的值(經常以ψ和∆或相關的量表示)。一次測量完成以後,所得的數據用來分析得到光學常數,膜層厚度,以及其他感興趣的參數值。如下圖所示,分析的過程包含很多步驟。
橢偏儀5
橢偏儀6
圖中的下一步,利用模型來生成Gen.Data,由模型確定的參數生成Psi和Detla數據,並與測量得到的數據進行比較,不斷修正模型中的參數使得生成的數據與測量得到的數據盡量一致。即使在一個大的基底上只有一層薄膜,理論上對這個模型的代數方程描述也是非常複雜的。因此通常不能對光學常數、厚度等給出類似上面方程一樣的數學描述,這樣的問題,通常被稱作是反演問題。
最通常的解決橢偏儀反演問題的方法就是在衰減分析中,應用Levenberg-Marquardt演演算法。利用比較方程,將實驗所得到的數據和模型生成的數據比較。通常,定義均方誤差為:
橢偏儀7
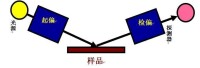
在光譜橢偏儀的測量中使用不同的硬體配置,但每種配置都必須能產生已知偏振態的光束。測量由被測樣品反射后光的偏振態。這要求儀器能夠量化偏振態的變化量ρ。
橢偏儀8
在選擇合適的橢偏儀的時候,光譜範圍和測量速度也是一個通常需要考慮的重要因素。可選的光譜範圍從深紫外的142nm到紅外的33microm。光譜範圍的選擇通常由應用決定。不同的光譜範圍能夠提供關於材料的不同信息,合適的儀器必須和所要測量的光譜範圍匹配。
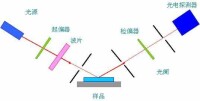
橢偏儀基本架構
橢偏儀 全自動光譜橢偏儀 成像橢偏儀(成像橢圓偏振技術)激光單波長橢偏儀……
最初,橢偏儀的工作波長多為單一波長或少數獨立的波長,最典型的是採用激光或對電弧等強光譜光進行濾光產生的單色光源。現在大多數的橢偏儀在很寬的波長範圍內以多波長工作(通常有幾百個波長,接近連續)。和單波長的橢偏儀相比,光譜型橢偏儀有下面的優點:可以提升多層探測能力,可以測試物質對不同波長光波的折射率等。
橢偏儀的光譜範圍在深紫外的142nm到紅外33um可選。光譜範圍的選擇取決於被測材料的屬性、薄膜厚度及關心的光譜段等因素。例如,摻雜濃度對材料紅外光學屬性有很大的影響,因此需要能測量紅外波段的橢偏儀;薄膜的厚度測量需要光能穿透這薄膜,到達基底,然後並被探測器檢測到,因此需要選用該待測材料透明或部分透明的光譜段;對於厚的薄膜選取長波長更有利於測量。
半導體、微電子、MEMS、通訊、數據存儲、光學鍍膜、平板顯示器、科學研究、物理、化學、生物、醫藥…
半導體、介電材料、有機高分子聚合物、金屬氧化物、金屬鈍化膜、自組裝單分子層、多層膜物質和石墨烯等等.
