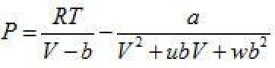立方型方程

立方型方程

立方型方程(CEOS, cubic equatiion of state)，因其公式展開求根過程總是出現V有3次冪而命名，其展開式通式為aV^3+bV^2+cV+d=0.

目錄

1由來 2CEOSs 3缺陷

由來

CEOS是經典熱力學狀態方程(EOS,equation of state)，其提出的依據

是分子間的力包括排斥力和吸引力:。通常斥力項>0，

引力項<0。其通過表達式為

CEOSs

CEOS方程的典型代表有標準的van der Walls、Redlich-Kwong(RK)、Peng-Robinson(PR)等等。下表為常見的CEOS。

Van der Waals (vdW)

Redlich-Kwong (RK)

Soave (SRK)

Peng-Robinson (PR)

Heyen (H)

Schmit-Wenzel (SW)

HCL

Harmens-Knapp (HK)

F

CEOS方程有原來的vdW變化而來，是普遍性規律，對於特定的目標會有較大的誤差，因為有各種修改的版本，主要修改集中在：

1. 採用更加複雜的引力項，例如RK在引力項中引入溫度，SRK和PR都引入溫度、偏心因子；

2. CEOS往往不能較為準確的預測液體體積，因此常常採用體積變化法修正誤差。原理是利用V+c代替原來的V；

缺陷

CEOS是經典的熱力學狀態方程，至今仍然十分具有活力，主要是因為該類方程形式簡單，表達式求根簡潔，規律性強。但是該類方程也具有比較突出的缺陷：

1. 在超臨界點附近預測誤差很大，主要從臨界壓縮因子可以看出，實際流體的，比最常見的PR 0.3074，SRK 來的小；

2. 預測液體體積能力不足；

3. 對複雜體系不適用，例如高分子體系

針對以上述原因，現在已經發展出很多的更加複雜、精確的狀態方程，如多參數狀態方程、統計熱力學狀態方程等等。

目錄