外彈道學
外彈道學
外彈道學研究彈丸或拋射體在空中的運動規律及有關現象的學科。是彈道學的一個分支。槍彈、炮彈、火箭彈和航空炸彈等在空中飛行時,由於受空氣阻力、地球引力和慣性力的作用,不斷改變其運動速度、方向和飛行姿態。火箭彈在其發動機工作期間,還將受到推力和推力矩的作用。不同的氣象條件也將對彈丸的運動產生影響。通常可以將彈丸的運動分解為質心運動和圍繞質心運動(繞心運動)兩部分,分別由動量定律和動量矩定律描述。
外彈道學的研究內容主要包括:彈丸或拋射體在飛行中的受力狀況,彈丸質心運動、繞心運動的規律及其影響因素,外彈道規律的實際應用等。它涉及理論力學、空氣動力學、大氣物理和地球物理等基礎學科領域,在武器彈藥的研究、設計、試驗和使用上佔有重要的地位。
外彈道學
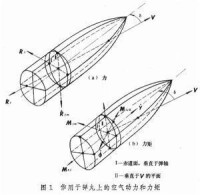
作用於彈丸的空氣動力與空氣的性質(溫度、壓力、粘性等)、彈丸的特性(形狀、大小等)、飛行姿態以及彈丸與空氣相對速度的大小等有關。當彈丸飛行速度矢量V與彈軸的夾角δ(稱為攻角或章動角)為零時,空氣對彈丸的總阻力R的方向與V相反,它使彈丸減速,稱為迎面阻力。當攻角不為零時,R可分解為與V方向相反的迎面阻力Rx和與V垂直的升力Ry,後者使彈丸向升力方向偏移。由於總阻力的作用點(稱為阻心或壓心)與彈丸的質心並非恰好重合,因而形成了一個靜力矩Mz。它使旋轉彈丸的攻角增大而使尾翼彈丸的攻角減少,因而分別稱為翻轉力矩和穩定力矩。當彈軸有擺動角速度時,彈丸周圍的空氣將產生阻滯其擺動的赤道阻尼力矩M;當彈丸有繞軸的自轉角速度時,將形成阻滯其自轉的極阻尼力矩Mxj。如自轉時有攻角存在,還將形成一個與攻角平面垂直的側向力和力矩,稱為馬格納斯力(Magnusforce)Rxm和馬格納斯力矩Mym。這些力和力矩如圖1所示。在諸空氣動力中,迎面阻力、升力和靜力矩對彈丸運動影響較大。式中的Сx、Сy、mz分別為阻力係數、升力係數和靜力矩係數。它們均為馬赫數M和攻角δ的函數;S、l、ρ分別為彈丸橫截面積、彈長和空氣密度。
此外,隨時間、地點和高度的不同而變化的氣象因素(如氣溫、氣壓和風等),將直接影響空氣的密度和彈丸與空氣的相對速度,使空氣動力發生變化。通常氣溫高、氣壓低或順風均會使射程增大,反之則減小。橫風將使彈丸側偏。但火箭彈道的主動段,由於有推力存在,風的影響規律比較複雜,與槍炮彈丸的彈道不同。
要準確地描述彈丸運動的規律,有賴於對上述空氣動力的準確測量,測量的方法通常有風洞法和射擊法兩類,後者已發展成為實驗外彈道學的主要內容。
在攻角為零、標準氣象條件和其他一些基本假設下,彈丸質心運動的軌跡將是一條平面曲線(理想彈道)。它由初速V0、射角θ0和彈道係數c(炸彈彈道還有投彈高度Η)完全確定。
彈道係數c是反映彈丸受空氣阻力影響大小的重要參量,c=id2×103/G,式中d、G分別為彈徑和彈重;I=cx(M)/cxon(M)稱為彈形係數,它是當攻角為零時彈丸阻力係數cx與某標準彈阻力係數cxon之比;M為馬赫數(彈丸速度與音速之比)。彈道係數越小,對減小阻力、增大射程越有利。在同樣的初速和射角條件下,彈道係數與射程的關係如圖2所示。圖中彈道係數是根據43年阻力定律得出的。
外彈道學
研究質心運動規律的目的,在於準確地獲得彈道上任意點的坐標、速度、彈道傾角和飛行時間等彈道諸元以及在非標準條件下的射擊修正量。由初速、射角和彈道係數(炸彈還有投彈高度)等參量可以編製外彈道表,用以直接查取或求得頂點、落點乃至任意點的彈道諸元和有關的修正係數。
火箭外彈道可分為有推力作用的主動段和無推力作用的被動段。被動段彈道與槍炮彈丸的彈道相同。在主動段內,火箭彈在發動機的推力作用下不斷加速飛行,到主動段末,其速度達最大值Vk。Vk的大小主要取決於火箭推進劑的性能,推進劑重量W與火箭彈的起始重量G0的比值W/G0和彈形等。
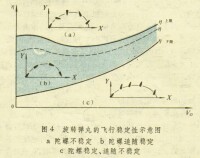
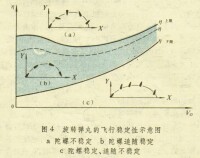
彈丸在作質心運動的同時作繞心運動。當攻角不大時,繞心運動可用線性理論來描述。起始擾動引起攻角的大小呈周期性變化。攻角平面在空中繞速度矢量旋轉,與攻角相應的升力矢量也將在空中旋轉,使彈丸質心運動的軌跡成為一條空中螺旋線。螺旋線的軸線向一方偏離形成平均偏角,它的大小和相應主要與隨機變化的起始擾動有關。這是造成跳角及其散布,特別是低伸彈道高低和方向散布的重要原因。由重力引起的非周期性變化的攻角稱為動力平衡角。它對於右(左)旋彈丸主要偏向彈道右(左)方,與其相應的升力產生使彈丸向右(左)側運動的偏流。此外,由於彈丸攻角大小的變化,還將引起迎面阻力的增大和變化,使射程減小併產生散布。對於尾翼穩定彈丸繞心運動對質心運動的影響,除了不形成偏流外,其他與旋轉彈丸相似。

外彈道學
外彈道學
外彈道設計計算
根據武器彈藥的戰術技術要求,應用空氣動力學、現代優化理論和計算技術對相應的外彈道方程組進行彈道計算,以尋求最有利的運動條件並確定出彈重、彈徑、初速和彈形結構等的合理值。綜合應用飛行穩定性和散布理論,提供滿足射程、射擊精度要求和減小散布的有利條件,尋求最優化的總體設計方案。它為武器、彈藥、引信等的設計、研究、試驗、使用提供依據。
編製射表與提供彈道數學模型
根據外彈道理論結合射擊(或投放)試驗,準確地列出特定武器的射角、射程及其他彈道諸元間的對應關係;應用修正理論給出相應彈道諸元在非標準條件下的修正量;用實驗和散布理論確定出有關的散布特徵量,為準確有效地實施射擊(或投放)提供依據(見射擊學)。準確完善的射表或簡單可靠的彈道數學模型是設計製作瞄準具、射擊指揮儀或武器火控系統等的基礎。
中國春秋戰國時期成書的《考工記》中,就有關於保持箭矢飛行穩定的詳細論述。如《考工記・矢人》說:箭干“夾其陰陽以設其比,夾其比以設其羽,叄分其羽以設其刃,則雖有疾風亦弗之能憚矣”“前弱則_,后弱則翔,中弱則紆,中強則揚,羽豐則遲,羽殺則_”,都是出於對箭矢飛行穩定性要求的考慮。
北宋時期,中國發明了以火藥作為動力的焰火火箭;13世紀開始使用以火藥為能源的射擊武器,傳入歐洲以後,有力地推動了彈丸運動的研究。
直至17世紀30年代,義大利科學家伽利略才從嚴格的數學、力學基礎上導出了只考慮恆定重力作用的真空彈道方程。1687年,英國物理學家I.牛頓第一個提出考慮空氣阻力的空氣彈道解法。1753年,瑞士數學家、力學家L.歐拉在實驗研究空氣阻力的基礎上,提出了適用於亞聲速(小於250米/秒)彈丸的平方阻力定律和彈道的近似分析解法──歐拉解法。之後,又出現過多種近似分析解法,如義大利F.西亞切提出了對亞聲速、跨聲速、超聲速同時適用的西亞切阻力定律和適用於低伸彈道的西亞切解法(西亞切_Ⅲ,1896),以及蘇聯的1943年阻力定律等。但對於大射角的高速彈道,還不能給出足夠準確的解。直到20世紀20年代,出現了數值積分法(如差分法、龍格_庫塔法等)以後,才得到一個較為準確的計算空氣彈道的普遍方法。
19世紀中期,長圓形彈體和線膛火炮使用后,旋轉穩定彈的偏流現象被發現,促使彈道學者建立起剛體彈道模型,研究飛行穩定性,並對考慮全部作用力和力矩的彈箭質心運動和繞心運動進行較深入的研究。在20世紀20年代前後,出現了以彈道係數、初速和射角為自變數的地面火炮外彈道表,可以方便地查算彈道諸元。此後,又出現了高射火炮外彈道表、用於槍及反坦克武器的低伸彈道表和用於投放炸彈的航空炸彈彈道表等。彈道表的內容也由基本諸元發展到基本諸元與修正諸元並列。火箭武器出現以前的外彈道學,實際上就是身管武器外彈道學。
第一次世界大戰中出現航空炸彈和魚雷以後,相應地促進了包含炸彈彈道在內的航空彈道學和研究魚雷在水中運動的水中彈道學的發展。第二次世界大戰中出現了以德國V_2彈道式火箭為代表的有控彈,此後研製了各種類型的導彈及其他靈巧彈,相應地開展了彈箭控制飛行過程的研究,拓展了外彈道學的研究領域。20世紀中後期,發展了研究潛地導彈、火箭助飛魚雷等兼有水下和空中彈道規律的雙介質彈道學。
第二次世界大戰後,由於測試技術和實驗彈道學的發展,特別是高速風洞和彈道靶道的建立,彈箭空氣動力學的研究有了新的突破,除改善了諸空氣動力係數的理論計算和實測的準確性外,還發現了在大攻角條件下的諸空氣動力的非線性問題,並創立了彈箭飛行動態穩定性理論。
