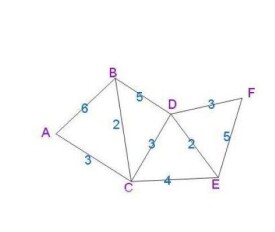
Floyd演演算法
加權圖中頂點間最短路徑的演演算法
Floyd演演算法(Floyd-Warshall algorithm)又稱為弗洛伊德演演算法、插點法,是解決給定的加權圖中頂點間的最短路徑的一種演演算法,可以正確處理有向圖或負權的最短路徑問題,同時也被用於計算有向圖的傳遞閉包。該演演算法名稱以創始人之一、1978年圖靈獎獲得者、斯坦福大學計算機科學系教授羅伯特·弗洛伊德命名。
通過一個圖的權值矩陣求出它的每兩點間的最短路徑矩陣。
從圖的帶權鄰接矩陣A=[a(i,j)] n×n開始,遞歸地進行n次更新,即由矩陣D(0)=A,按一個公式,構造出矩陣D(1);又用同樣地公式由D(1)構造出D(2);……;最後又用同樣的公式由D(n-1)構造出矩陣D(n)。矩陣D(n)的i行j列元素便是i號頂點到j號頂點的最短路徑長度,稱D(n)為圖的距離矩陣,同時還可引入一個後繼節點矩陣path來記錄兩點間的最短路徑。
採用鬆弛技術(鬆弛操作),對在i和j之間的所有其他點進行一次鬆弛。所以時間複雜度為O(n^3);
其狀態轉移方程如下: map[i,j]:=min{map[i,k]+map[k,j],map[i,j]};
map[i,j]表示i到j的最短距離,K是窮舉i,j的斷點,map[n,n]初值應該為0,或者按照題目意思來做。
當然,如果這條路沒有通的話,還必須特殊處理,比如沒有map[i,k]這條路。
1,從任意一條單邊路徑開始。所有兩點之間的距離是邊的權,如果兩點之間沒有邊相連,則權為無窮大。
2,對於每一對頂點 u 和 v,看看是否存在一個頂點 w 使得從 u 到 w 再到 v 比已知的路徑更短。如果是更新它。
把圖用鄰接矩陣G表示出來,如果從Vi到Vj有路可達,則G[i,j]=d,d表示該路的長度;否則G[i,j]=無窮大。定義一個矩陣D用來記錄所插入點的信息,D[i,j]表示從Vi到Vj需要經過的點,初始化D[i,j]=j。把各個頂點插入圖中,比較插點后的距離與原來的距離,G[i,j] = min( G[i,j], G[i,k]+G[k,j] ),如果G[i,j]的值變小,則D[i,j]=k。在G中包含有兩點之間最短道路的信息,而在D中則包含了最短通路徑的信息。
比如,要尋找從V5到V1的路徑。根據D,假如D(5,1)=3則說明從V5到V1經過V3,路徑為{V5,V3,V1},如果D(5,3)=3,說明V5與V3直接相連,如果D(3,1)=1,說明V3與V1直接相連。
Floyd演演算法適用於APSP(All Pairs Shortest Paths,多源最短路徑),是一種動態規劃演演算法,稠密圖效果最佳,邊權可正可負。此演演算法簡單有效,由於三重循環結構緊湊,對於稠密圖,效率要高於執行|V|次Dijkstra演演算法,也要高於執行V次SPFA演演算法。
優點:容易理解,可以算出任意兩個節點之間的最短距離,代碼編寫簡單。
缺點:時間複雜度比較高,不適合計算大量數據。
a)初始化:D[u,v]=A[u,v]
b)For k:=1 to n
For i:=1 to n
For j:=1 to n
If D[i,j]>D[i,k]+D[k,j] Then
D[i,j]:=D[i,k]+D[k,j];
c)演演算法結束:D即為所有點對的最短路徑矩陣
#include
#include
#define max 1000000000;
int a,d;
int main(){
int i,j,k,m,n;
int x,y,z;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
a[x][y]=z;
}
for(i=1;i<=m;i++)
for(j=1;j<=m;j++)
d[i][j]=max;
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++){
if(a[i][k]+a[k][j]
d[i][j]=a[i][k]+a[k][j];
}
for(i=1;i<=m;i++)
printf("%d ",d[i]);
return 0;
}
#include
#define Maxm 501
using namespace std;
ifstreamfin;ofstreamfout("APSP.out");
int p,q,k,m;
intVertex,Line[Maxm];
intPath[Maxm][Maxm],Dist[Maxm][Maxm];
voidRoot(intp,intq){
if(Path[p][q]>0){
Root(p,Path[p][q]);
Root(Path[p][q],q);
}
else{Line[k]=q;k++;
}
}int main(){memset(Path,0,sizeof(Path));
memset(Dist,0,sizeof(Dist));
fin>>Vertex;
for(p=1;p<=Vertex;p++)
for(q=1;q<=Vertex;q++)
fin>>Dist[p][q];
for(k=1;k<=Vertex;k++)
for(p=1;p<=Vertex;p++)
if(Dist[p][k]>0)
for(q=1;q<=Vertex;q++)
if(Dist[k][q]>0){
if(((Dist[p][q]>Dist[p][k]+Dist[k][q])||(Dist[p][q]==0))&&(p!=q)){
Dist[p][q]=Dist[p][k]+Dist[k][q];
Path[p][q]=k;
}
}for(p=1;p<=Vertex;p++){
for(q=p+1;q<=Vertex;q++){
fout<<"\n==========================\n";
fout<<"Source:"<
<<'\n'<<"Target"<<<'\n';
fout<<"Distance:"<<<'\n';fout<<"Path:"<
for(m=2;m<=k-1;m++)fout<<"-->"<
}
}fin.close();
fout.close();
return0;
}
註解:無法連通的兩個點之間距離為0;
Sample Input
7
00 20 50 30 00 00 00
20 00 25 00 00 70 00
50 25 00 40 25 50 00
30 00 40 00 55 00 00
00 00 25 55 00 10 70
00 70 50 00 10 00 50
00 00 00 00 70 5000
Sample Output
==========================
Source:1
Target 2
Distance:20
Path:1-->2
==========================
==========================
Source:1
Target 3
Distance:45
Path:1-->2-->3
==========================
==========================
Source:1
Target 4
Distance:30
Path:1-->4
==========================
==========================
Source:1
Target 5
Distance:70
Path:1-->2-->3-->5
==========================
==========================
Source:1
Target 6
Distance:80
Path:1-->2-->3-->5-->6
==========================
==========================
Source:1
Target 7
Distance:130
Path:1-->2-->3-->5-->6-->7
==========================
==========================
Source:2
Target 3
Distance:25
Path:2-->3
==========================
==========================
Source:2
Target 4
Distance:50
Path:2-->1-->4
==========================
==========================
Source:2
Target 5
Distance:50
Path:2-->3-->5
==========================
==========================
Source:2
Target 6
Distance:60
Path:2-->3-->5-->6
==========================
==========================
Source:2
Target 7
Distance:110
Path:2-->3-->5-->6-->7
==========================
==========================
Source:3
Target 4
Distance:40
Path:3-->4
==========================
==========================
Source:3
Target 5
Distance:25
Path:3-->5
==========================
==========================
Source:3
Target 6
Distance:35
Path:3-->5-->6
==========================
==========================
Source:3
Target 7
Distance:85
Path:3-->5-->6-->7
==========================
==========================
Source:4
Target 5
Distance:55
Path:4-->5
==========================
==========================
Source:4
Target 6
Distance:65
Path:4-->5-->6
==========================
==========================
Source:4
Target 7
Distance:115
Path:4-->5-->6-->7
==========================
==========================
Source:5
Target 6
Distance:10
Path:5-->6
==========================
==========================
Source:5
Target 7
Distance:60
Path:5-->6-->7
==========================
==========================
Source:6
Target 7
Distance:50
Path:6-->7
function Floyd(w,router_direction,MAX)
%x為此圖的距離矩陣
%router_direction為路由類型:0為前向路由;非0為回溯路由
%MAX是數據輸入時的∞的實際值
len=length(w);
flag=zeros(1,len);
%根據路由類型初始化路由表
R=zeros(len,len);
for i=1:len
if router_direction==0%前向路由
R(:,i)=ones(len,1)*i;
else %回溯路由
R(i,:)=ones(len,1)*i;
end
R(i,i)=0;
end
disp('');
disp('w(0)');
dispit(w,0);
disp('R(0)');
dispit(R,1);
%處理端點有權的問題
for i=1:len
tmp=w(i,i)/2;
if tmp~=0
w(i,:)=w(i,:)+tmp;
w(:,i)=w(:,i)+tmp;
flag(i)=1;
w(i,i)=0;
end
end
%Floyd演演算法具體實現過程
for i=1:len
for j=1:len
if j==i||w(j,i)==MAX
continue;
end
for k=1:len
if k==i||w(j,i)==MAX
continue;
end
if w(j,i)+w(i,k)
w(j,k)=w(j,i)+w(i,k);
if router_direction==0%前向路由
R(j,k)=R(j,i);
else %回溯路由
R(j,k)=R(i,k);
end
end
end
end
%顯示每次的計算結果
disp(['w(',num2str(i),')'])
dispit(w,0);
disp(['R(',num2str(i),')'])
dispit(R,1);
end
%中心和中點的確定
[Center,index]=min(max(w'));
disp(['中心是V',num2str(index)]);
[Middle,index]=min(sum(w'));
disp(['中點是V',num2str(index)]);
end
function dispit(x,flag)
%x:需要顯示的矩陣
%flag:為0時表示顯示w矩陣,非0時表示顯示R矩陣
len=length(x);
s=[];
for j=1:len
if flag==0
s=[s sprintf('%5.2f\t',x(j,:))];
else
s=[s sprintf('%d\t',x(j,:))];
end
s=[s sprintf('\n')];
end
disp(s);
disp('---------------------------------------------------');
end
% 選擇后按Ctrl+t取消註釋號%
%
% 示例:
% a=[
% 0,100,100,1.2,9.2,100,0.5;
% 100,0,100,5,100,3.1,2;
% 100,100,0,100,100,4,1.5;
% 1.2,5,100,0,6.7,100,100;
% 9.2,100,100,6.7,0,15.6,100;
% 100,3.1,4,100,15.6,0,100;
% 0.5,2,1.5,100,100,100,0
% ];
%
% b=[
% 0,9.2,1.1,3.5,100,100;
% 1.3,0,4.7,100,7.2,100;
% 2.5,100,0,100,1.8,100;
% 100,100,5.3,0,2.4,7.5;
% 100,6.4,2.2,8.9,0,5.1;
% 7.7,100,2.7,100,2.1,0
% ];
%
% Floyd(a,1,100)
% Floyd(b,1,100)
program floyd;
var
st,en,f:integer;
k,n,i,j,x:integer;
a:array[1..10,1..10] of integer;
path:array[1..10,1..10] of integer;
begin
readln(n);
for i:=1 to n do
begin
for j:=1 to n do
begin
read(k);
if k<>0 then
a[i,j]:=k
else
a[i,j]:=maxint;
path[i,j]:=j;
end;
readln;
end;
for x:=1 to n do
for i:=1 to n do
for j:=1 to n do
if a[i,j]>a[i,x]+a[x,j] then
begin
a[i,j]:=a[i,x]+a[x,j];
path[i,j]:=path[i,x];
end;
readln(st,en);
writeln(a[st,en]);
f:=st;
while f<> en do
begin
write(f);
write('-->');
f:=path[f,en];
end;
writeln(en);
end.
//以無向圖G為入口,得出任意兩點之間的路徑長度length[i][j],路徑path[i][j][k],
//途中無連接得點距離用0表示,點自身也用0表示
public class FLOYD {
int[][] length = null;// 任意兩點之間路徑長度
int[][][] path = null;// 任意兩點之間的路徑
public FLOYD(int[][] G) {
int MAX = 100;int row = G.length;// 圖G的行數
int[][] spot = new int[row][row];// 定義任意兩點之間經過的點
int[] onePath = new int[row];// 記錄一條路徑
length = new int[row][row];
path = new int[row][row][];
for (int i = 0; i < row; i++)// 處理圖兩點之間的路徑
for (int j = 0; j < row; j++) {
if (G[i][j] == 0)G[i][j] = MAX;// 沒有路徑的兩個點之間的路徑為默認最大
if (i == j)G[i][j] = 0;// 本身的路徑長度為0
}
for (int i = 0; i < row; i++)// 初始化為任意兩點之間沒有路徑
for (int j = 0; j < row; j++)
spot[i][j] = -1;
for (int i = 0; i < row; i++)// 假設任意兩點之間的沒有路徑
onePath[i] = -1;
for (int v = 0; v < row; ++v)
for (int w = 0; w < row; ++w)
length[v][w] = G[v][w];
for (int u = 0; u < row; ++u)
for (int v = 0; v < row; ++v)
for (int w = 0; w < row; ++w)
if (length[v][w] > length[v][u] + length[u][w]) {
length[v][w] = length[v][u] + length[u][w];// 如果存在更短路徑則取更短路徑
spot[v][w] = u;// 把經過的點加入
}
for (int i = 0; i < row; i++) {// 求出所有的路徑
int[] point = new int;
for (int j = 0; j < row; j++) {
point = 0;
onePath[point++] = i;
outputPath(spot, i, j, onePath, point);
path[i][j] = new int[point];
for (int s = 0; s < point; s++)
path[i][j][s] = onePath[s];
}
}
}
void outputPath(int[][] spot, int i, int j, int[] onePath, int[] point) {// 輸出i// 到j// 的路徑的實際代碼,point[]記錄一條路徑的長度
if (i == j)return;
if (spot[i][j] == -1)
onePath[point++] = j;
// System.out.print(" "+j+" ");
else {
outputPath(spot, i, spot[i][j], onePath, point);
outputPath(spot, spot[i][j], j, onePath, point);
}
}
public static void main(String[] args) {
int data[][] = {
{ 0, 27, 44, 17, 11, 27, 42, 0, 0, 0, 20, 25, 21, 21, 18, 27, 0 },// x1
{ 27, 0, 31, 27, 49, 0, 0, 0, 0, 0, 0, 0, 52, 21, 41, 0, 0 },// 1
{ 44, 31, 0, 19, 0, 27, 32, 0, 0, 0, 47, 0, 0, 0, 32, 0, 0 },// 2
{ 17, 27, 19, 0, 14, 0, 0, 0, 0, 0, 30, 0, 0, 0, 31, 0, 0 },// 3
{ 11, 49, 0, 14, 0, 13, 20, 0, 0, 28, 15, 0, 0, 0, 15, 25, 30 },// 4
{ 27, 0, 27, 0, 13, 0, 9, 21, 0, 26, 26, 0, 0, 0, 28, 29, 0 },// 5
{ 42, 0, 32, 0, 20, 9, 0, 13, 0, 32, 0, 0, 0, 0, 0, 33, 0 },// 6
{ 0, 0, 0, 0, 0, 21, 13, 0, 19, 0, 0, 0, 0, 0, 0, 0, 0 },// 7
{ 0, 0, 0, 0, 0, 0, 0, 19, 0, 11, 20, 0, 0, 0, 0, 33, 21 },// 8
{ 0, 0, 0, 0, 28, 26, 32, 0, 11, 0, 10, 20, 0, 0, 29, 14, 13 },// 9
{ 20, 0, 47, 30, 15, 26, 0, 0, 20, 10, 0, 18, 0, 0, 14, 9, 20 },// 10
{ 25, 0, 0, 0, 0, 0, 0, 0, 0, 20, 18, 0, 23, 0, 0, 14, 0 },// 11
{ 21, 52, 0, 0, 0, 0, 0, 0, 0, 0, 0, 23, 0, 27, 22, 0, 0 },// 12
{ 21, 21, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 27, 0, 0, 0, 0 },// 13
{ 18, 41, 32, 31, 15, 28, 0, 0, 0, 29, 14, 0, 22, 0, 0, 11, 0 },// 14
{ 27, 0, 0, 0, 25, 29, 33, 0, 33, 14, 9, 14, 0, 0, 11, 0, 9 },// 15
{ 0, 0, 0, 0, 30, 0, 0, 0, 21, 13, 20, 0, 0, 0, 0, 9, 0 } // 16
};
for (int i = 0; i < data.length; i++)
for (int j = i; j < data.length; j++)
if (data[i][j] != data[j][i])return;
FLOYD test=new FLOYD(data);
for (int i = 0; i < data.length; i++)
for (int j = i; j < data[i].length; j++) {
System.out.println();
System.out.print("From " + i + " to " + j + " path is: ");
for (int k = 0; k < test.path[i][j].length; k++)
System.out.print(test.path[i][j][k] + " ");
System.out.println();
System.out.println("From " + i + " to " + j + " length :"+ test.length[i][j]);
}
}
}