曲線積分

先看一個例子：設有一曲線形構件佔xOy面上的一段曲線，設構件的密度分佈函數為定義在L上且在L上連續，求構件的質量。對於密度均勻的物件可以直接用ρV求得質量；對於密度不均勻的物件，就需要用到曲線積分,；L是積分路徑就叫做對弧長的曲線積分。

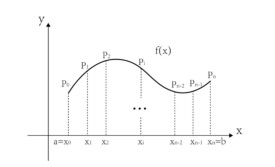
設L為xOy平面上的一條光滑的簡單曲線弧，在L上有界，在L上任意插入一點列把L分成n個小弧段的長度為ds，又是L上的任一點，作乘積，並求和即，記，若的極限在當λ→0的時候存在，且極限值與L的分法及在L的取法無關，則稱極限值為在L上對弧長的曲線積分，記為：；其中叫做被積函數，L叫做積分曲線，對弧長的曲線積分也叫第一類曲線積分。

（上述定義並不完全嚴謹，給出新的定義）：在矢量場A中，任取一連接點P0與P1的光滑曲線c，此時向量記作R0，向量記作R1，用ΔR表示位於曲線C的切線上，以切點為始點而模(其中ΔR為粗體）等於弧元ΔR的小矢量，作標積，A是ΔR始點的矢量，是A在弧的切線上的投影。將所有弧元ΔR的標積相加，並使弧元數量無限制增加且使得每一弧元長度趨向於0，求U的極限，所以。稱U為矢量A沿曲線c的曲線積分。

曲線積分分為：

（1）對弧長的曲線積分（第一類曲線積分）

（2）對坐標軸的曲線積分（第二類曲線積分）

兩種曲線積分的區別主要在於積分元素的差別；對弧長的曲線積分的積分元素是弧長元素ds；例如：對L的曲線積分。對坐標軸的曲線積分的積分元素是坐標元素dx或dy，例如：對L’的曲線積分。但是對弧長的曲線積分由於有物理意義，通常說來都是正的，而對坐標軸的曲線積分可以根據路徑的不同而取得不同的符號。

對弧長的曲線積分和對坐標軸的曲線積分是可以互相轉化的，利用弧微分公式，或者；這樣對弧長的曲線積分都可以轉換成對坐標軸的曲線積分了。

在曲線積分中，被積的函數可以是標量函數或向量函數。積分的值是路徑各點上的函數值乘上相應的權重（一般是弧長，在積分函數是向量函數時，一般是函數值與曲線微元向量的標量積）后的黎曼和。帶有權重是曲線積分與一般區間上的積分的主要不同點。物理學中的許多簡單的公式（比如說）在推廣之後都是以曲線積分的形式出現（）。曲線積分在物理學中是很重要的工具，例如計算電場或重力場中的做功，或量子力學中計算粒子出現的概率。

量子力學中的“曲線積分形式”和曲線積分並不相同，因為曲線積分形式中所用的積分是函數空間上的泛函積分，即關於空間中每個路徑的概率函數進行積分。然而，曲線積分在量子力學中仍有重要作用，比如說復圍道積分常常用來計算量子散射理論中的概率振幅。

如果將複數看作二維的向量，那麼二維向量場的曲線積分就是相應複函數的共軛函數在同樣路徑上的積分值的實部。根據柯西-黎曼方程，一個全純函數的共軛函數所對應的向量場的旋度是0。

在各種保守力的場都是路徑無關的，一個常見的例子就是重力場或電場。在計算這種場的做功時，可以選擇適當的路徑進行積分，使得計算變得簡單。如：。徠