積分
數學術語
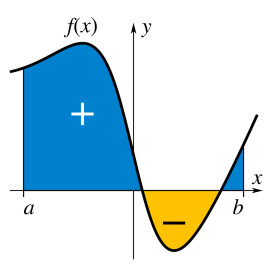
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函數,在一個實數區間上的定積分可以理解為在坐標平面上,由曲線、直線以及軸圍成的曲邊梯形的面積值(一種確定的實數值)。
積分的一個嚴格的數學定義由波恩哈德·黎曼給出(參見條目“黎曼積分”)。黎曼的定義運用了極限的概念,把曲邊梯形設想為一系列矩形組合的極限。從十九世紀起,更高級的積分定義逐漸出現,有了對各種積分域上的各種類型的函數的積分。比如說,路徑積分是多元函數的積分,積分的區間不再是一條線段(區間[a,b]),而是一條平面上或空間中的曲線段;在面積積分中,曲線被三維空間中的一個曲面代替。對微分形式的積分是微分幾何中的基本概念。
積分發展的動力源自實際應用中的需求。實際操作中,有時候可以用粗略的方式進行估算一些未知量,但隨著科技的發展,很多時候需要知道精確的數值。要求簡單幾何形體的面積或體積,可以套用已知的公式。比如一個長方體狀的游泳池的容積可以用長×寬×高求出。但如果游泳池是卵形、拋物型或更加不規則的形狀,就需要用積分來求出容積。物理學中,常常需要知道一個物理量(比如位移)對另一個物理量(比如力)的累積效果,這時也需要用到積分。
如果一個函數的積分存在,並且有限,就說這個函數是可積的。一般來說,被積函數不一定只有一個變數,積分域也可以是不同維度的空間,甚至是沒有直觀幾何意義的抽象空間。如同上面介紹的,對於只有一個變數x的實值函數f,f在閉區間[a,b]上的積分記作
其中的 除了表示x是f中要進行積分的那個變數(積分變數)之外,還可以表示不同的含義。在黎曼積分中,表示分割區間的標記;在勒貝格積分中,表示一個測度;或僅僅表示一個獨立的量(微分形式)。一般的區間或者積分範圍J,J上的積分可以記作
如果變數不只一個,比如說在二重積分中,函數 在區域D上的積分記作 或者 其中
與區域D對應,是相應積分域中的微分元。
方法不止一種,各種定義之間也不是完全等價的。其中的差別主要是在定義某些特殊的函數:在某些積分的定義下這些函數不可積分,但在另一些定義之下它們的積分存在。然而有時也會因為教學的原因造成定義上的差別。最常見的積分定義是黎曼積分和勒貝格積分。

積分
黎曼積分得名於德國數學家波恩哈德·黎曼,建立在函數在區間取樣分割后的黎曼和之上。設有閉區間[a,b],那麼[a,b]的一個分割是指在此區間中取一個有限的點列。每個閉區間 叫做一個子區間。定義 為這些子區間長度的最大值: ,其中。而閉區間[a,b]上的一個取樣分割是指在進行分割 后,於每一個子區間中 取出一點。
對一個在閉區間[a,b]有定義的實值函數f,f關於取樣分割 的黎曼和定義為以下和式:
和式中的每一項是子區間長度 與在 處的函數值 的乘積。直觀地說,就是以標記點 到X軸的距離為高,以分割的子區間為長的矩形的面積。
最簡單的取樣分割方法是將區間均勻地分成若干個長度相等的子區間,然後在每個子區間上按相同的準則取得標記點。例如取每個子區間右端(見左圖左上角)或者取每個子區間上函數的極大值對應的(左圖左下角)等等。不同的取樣分割方式得到的黎曼和一般都不相同,而如果當 足夠小的時候,所有的黎曼和都趨於某個極限,那麼這個極限就叫做函數f在閉區間[a,b]上的黎曼積分。即,S是函數f在閉區間[a,b]上的黎曼積分,當且僅當對於任意的,都存在,使得對於任意的取樣分割,只要它的子區間長度最大值,就有:
也就是說,對於一個函數f,如果在閉區間[a,b]上,無論怎樣進行取樣分割,只要它的子區間長度最大值足夠小,函數f的黎曼和都會趨向於一個確定的值S,那麼f在閉區間[a,b]上的黎曼積分存在,並且定義為黎曼和的極限S。這時候稱函數f為黎曼可積的。將f在閉區間[a,b]上的黎曼積分記作:
勒貝格積分的出現源於概率論等理論中對更為不規則的函數的處理需要。黎曼積分無法處理這些函數的積分問題。因此,需要更為廣義上的積分概念,使得更多的函數能夠定義積分。同時,對於黎曼可積的函數,新積分的定義不應當與之衝突。勒貝格積分就是這樣的一種積分。黎曼積分對初等函數和分段連續的函數定義了積分的概念,勒貝格積分則將積分的定義推廣到測度空間里。
勒貝格積分的概念定義在測度的概念上。測度是日常概念中測量長度、面積的推廣,將其以公理化的方式定義。黎曼積分實際可以看成是用一系列矩形來儘可能鋪滿函數曲線下方的圖形,而每個矩形的面積是長乘寬,或者說是兩個區間之長度的乘積。測度為更一般的空間中的集合定義了類似長度的概念,從而能夠“測量”更不規則的函數曲線下方圖形的面積,從而定義積分。在一維實空間中,一個區間A= [a,b] 的勒貝格測度μ(A)是區間的右端值減去左端值,b−a。這使得勒貝格積分和正常意義上的黎曼積分相兼容。在更複雜的情況下,積分的集合可以更加複雜,不再是區間,甚至不再是區間的交集或並集,其“長度”則由測度來給出。
給定一個集合 上的 代數 以及 上的一個測度,那麼對於中的一個元素,定義指示函數 關於測度的積分為:
再定義可測的非負簡單函數(其中)的積分為:
對於一般的函數,如果對每個區間(a,b],都滿足,那麼測度論中定義f是可測函數。對於一個非負的可測函數f,它的積分定義為:為簡單函數,並且
恆大於零 這個積分可以用以下的方式逼近:
直觀上,這種逼近方式是將f的值域分割成等寬的區段,再考察每段的“長度”,用其測度表示,再乘以區段所在的高度。
至於一般的(有正有負的)可測函數f,它的積分是函數曲線在x軸上方“圍出”的面積,減去曲線在x軸下方“圍出”的面積。嚴格定義需要引進“正部函數”和“負部函數”的概念:
如果 則 否則
如果 則 否則
可以驗證,總有 而f的積分定義為: 。以上定義有意義僅當 和 中至少有一個的值是有限的(否則會出現無窮大減無窮大的情況),這時稱f的勒貝格積分存在或積分有意義。如果 和 都是有限的,那麼稱f可積。
給定一個可測集合A,可以定義可積函數在A上的積分為:
除了黎曼積分和勒貝格積分以外,還有若干不同的積分定義,適用於不同種類的函數。
達布積分:等價於黎曼積分的一種定義,比黎曼積分更加簡單,可用來幫助定義黎曼積分。
黎曼-斯蒂爾傑斯積分:黎曼積分的推廣,用一般的函數g(x)代替x作為積分變數,也就是將黎曼和中的 推廣為。
勒貝格-斯蒂爾傑斯積分:勒貝格積分的推廣,推廣方式類似於黎曼-斯蒂爾傑斯積分,用有界變差函數g代替測度。
哈爾積分:由阿爾弗雷德·哈爾於1933年引入,用來處理局部緊拓撲群上的可測函數的積分,參見哈爾測度。
積分都滿足一些基本的性質。 在黎曼積分意義上表示一個區間,在勒貝格積分意義下表示一個可測集合。
積分是線性的。如果一個函數f可積,那麼它乘以一個常數后仍然可積。如果函數f和g可積,那麼它們的和與差也可積。
所有在 上可積的函數構成了一個線性空間。黎曼積分的意義上,所有區間[a,b]上黎曼可積的函數f和g都滿足:
所有在可測集合上勒貝格可積的函數f和g都滿足:
在積分區域上,積分有可加性。黎曼積分意義上,如果一個函數f在某區間上黎曼可積,那麼對於區間內的三個實數a, b, c,有
如果函數f在兩個不相交的可測集 和 上勒貝格可積,那麼
如果函數f勒貝格可積,那麼對任意,都存在,使得 中任意的元素A,只要,就有
如果一個函數f在某個區間上黎曼可積,並且在此區間上大於等於零。那麼它在這個區間上的積分也大於等於零。如果f勒貝格可積並且幾乎總是大於等於零,那麼它的勒貝格積分也大於等於零。作為推論,如果兩個 上的可積函數f和g相比,f(幾乎)總是小於等於g,那麼f的(勒貝格)積分也小於等於g的(勒貝格)積分。
如果黎曼可積的非負函數f在 上的積分等於0,那麼除了有限個點以外, 。如果勒貝格可積的非負函數f在 上的積分等於0,那麼f幾乎處處為0。如果 中元素A的測度 等於0,那麼任何可積函數在A上的積分等於0。
函數的積分表示了函數在某個區域上的整體性質,改變函數某點的取值不會改變它的積分值。對於黎曼可積的函數,改變有限個點的取值,其積分不變。
對於勒貝格可積的函數,某個測度為0的集合上的函數值改變,不會影響它的積分值。如果兩個函數幾乎處處相同,那麼它們的積分相同。
如果對中任意元素A,可積函數f在A上的積分總等於(大於等於)可積函數g在A上的積分,那麼f幾乎處處等於(大於等於)g。
如果f在 上可積,M和m分別是f在上的最大值和最小值,那麼:
其中的 在黎曼積分中表示區間 的長度,在勒貝格積分中表示的測度。
● 黎曼積分
● 達布積分
● 勒貝格積分
● 黎曼-斯蒂爾吉斯積分
● 數值積分
● 微積分基本定理
● 不定積分
● 定積分
● 積分符號
● 積分表