正切
三角函數中的定義
在Rt△ABC(直角三角形)中,∠C=90°,AB是∠C的對邊c,BC是∠A的對邊a,AC是∠B的對邊b,正切函數就是tanB=b/a,即tanB=AC/BC。
三角函數是數學中屬於初等函數中的超越函數的一類函數。它們的本質是任意角的集合與一個比值的集合的變數之間的映射。通常的三角函數是在平面直角坐標系中定義的,其定義域為整 個實數域。另一種定義是在直角三角形中,但並不完全。現代數學把它們描述成無窮數列的極限和微分方程的解,將其定義擴展到複數系。
個實數域。另一種定義是在直角三角形中,但並不完全。現代數學把它們描述成無窮數列的極限和微分方程的解,將其定義擴展到複數系。

正切
由於三角函數的周期性,它並不具有單值函數意義上的反函數。
三角函數在複數中有較為重要的應用。在物理學中,三角函數也是常用的工具。
在Rt△ABC中,如果銳角A確定,那麼角A的對邊與鄰邊的比值隨之確定,這個比叫做角A的正切,記作tanA。
即:tanA=∠A的對邊/∠A的鄰邊。
函數名 正弦函數 餘弦函數 正切函數 餘切函數 正割函數 餘割函數
正弦函數 sinθ=y/r
餘弦函數 cosθ=x/r
正切函數 tanθ=y/x
餘切函數 cotθ=x/y
正割函數 secθ=r/x
餘割函數 cscθ=r/y
(1)平方關係:
sin^2(α)+cos^2(α)=1
tan^2(α)+1=sec^2(α)
cot^2(α)+1=csc^2(α)
(2)積的關係:
sinα=tanα*cosα cosα=cotα*sinα
tanα=sinα*secα cotα=cosα*cscα
secα=tanα*cscα cscα=secα*cotα
(3)倒數關係:
tanα·cotα=1
sinα·cscα=1
cosα·secα=1
兩角和與差的三角函數:
cos(α+β)=cosα·cosβ-sinα·sinβ
cos(α-β)=cosα·cosβ+sinα·sinβ
sin(α±β)=sinα·cosβ±cosα·sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
sin(2α)=2sinα·cosα
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
tan(2α)=2tanα/[1-tan^2(α)]
sin3α=3sinα-4sin^3(α)
cos3α=4cos^3(α)-3cosα
sin^2(α/2)=(1-cosα)/2
cos^2(α/2)=(1+cosα)/2
tan^2(α/2)=(1-cosα)/(1+cosα)
tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα
sin^2(α)=(1-cos(2α))/2
cos^2(α)=(1+cos(2α))/2
tan^2(α)=(1-cos(2α))/(1+cos(2α))
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
tanA·tanB·tan(A+B)+tanA+tanB-tan(A+B)=0
高等代數中三角函數的指數表示(由泰勒級數易得):
sinx=[e^(ix)-e^(-ix)]/(2i)
cosx=[e^(ix)+e^(-ix)]/2
tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]
tanA·tanB=1
定義域:{x|x≠(π/2)+kπ,k∈Z}
值域:R
奇偶性:有,為奇函數
周期性:有
最小正周期:kπ,k∈Z
單調性:有
單調增區間:(-π/2+kπ,+π/2+kπ),k∈Z
單調減區間:無
| tan15° | 2-√3 |
| tan30° | √3/3 |
| tan45° | 1 |
| tan60° | √3 |
| tan75° | 2+√3 |
在平面三角形中,正切定理說明任意兩條邊的和除以第一條邊減第二條邊的差所得的商等於這兩條邊的對角的和的一半的正切除以第一條邊對角減第二條邊對角的差的一半的正切所得的商。
法蘭西斯·韋達(François Viète)曾在他對三角法研究的第一本著作《應用於三角形的數學法則》中提出正切定理。現代的中學課本已經甚少提及,例如由於中華人民共和國曾經對前蘇聯和其教育學的批判,在1966年至1977年間曾經將正切定理刪除出中學數學教材。不過在沒有計算機的輔助求解三角形時,這定理可比餘弦定理更容易利用對數來運算投影等問題。
正切定理: (a + b) / (a - b) = tan((α+β)/2) / tan((α-β)/2)
證明 由下式開始:
由正弦定理得出
(參閱三角恆等式)
正切函數是直角三角形中,對邊與鄰邊的比值。放在直角坐標系中(如圖)即 tanθ=y/x
也有表示為tgθ=y/x,但一般常用tanθ=y/x(由正切英文tangent(讀作英[ˈtændʒənt] 美[ˈtændʒənt])簡寫得來)。曾簡寫為tg,現已停用,僅在20世紀90年代以前出版的書籍中使用。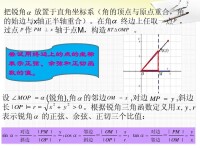

正切
