頻率解析度

頻率解析度是數字信號處理課程教學中一個重要的概念，因為它決定了DFT參數的選擇。

在現有的數字信號處理的書籍中，一般認為DFT頻率解析度為。

頻率解析度是指所用的演演算法能將信號中兩個靠得很近的譜峰保持分開的能力。

實際應用時，可以將頻率解析度理解為頻譜圖中，在頻率軸（頻譜圖的水平軸)）上得到的最小頻率間隔如果採樣頻率為fs，採樣時間間隔為t，採樣點數為N，採樣時間為t（完成一組樣本的採集所需要的時間），則頻率解析度為：

頻率解析度可以理解為在使用DFT時，在頻率軸上的所能得到的最小頻率間隔，其中為採樣點數，為採樣頻率，為採樣間隔。所以就是採樣前模擬信號的時間長度T，所以信號長度越長，頻率解析度越好。

採樣點數的多少與要求多大的頻率解析度有關。

例如：機器轉速，如果要分析的故障頻率估計在8倍頻以下，要求譜圖上頻率解析度，則採樣頻率和採樣點數設置為：

最高分析頻率；

採樣頻率；

採樣點數

譜線數

按照FFT變換，實際上得到的也是1024點的譜線，但是我們知道數學計算上存在負頻率，是對稱的，因此，實際上我們關注的是正頻率部分對應的譜線，也就是說正頻率有512線，為什麼我們通常又說這種情況下是400線呢，就是因為通常情況下由於頻率混疊和時域截斷的影響，通常認為401線到512線的頻譜精度不高而不予考慮。

另外，採樣點數也不是隨便設置的，即不是越大越好，反之亦然

對於旋轉機械必須滿足整周期採樣，以消除頻率畸形，單純提高解析度也不能消除頻率畸形

過去，有人以為數據越長越好，或隨便定時域信號長度，其實，這樣做是在某些概念上不清楚，例如，不清楚整周期採樣。不產生頻率混迭的最低採樣頻率Fs要求在2倍最大分析頻率Fm，之所以採用2.56倍主要跟計算機二進位的表示方式有關。其主要目的是避免信號混淆保證高頻信號不被歪曲成低頻信號。

採樣長度T的選擇首先要保證能反映信號的全貌，對瞬態信號應包括整個瞬態過程；對周期信號，理論上採集一個周期信號就可以了。其次需考慮頻率分辯率，採樣長度T在最大分析頻率確定的情況下與頻率分辯率是反比關係，也就是越長越小即頻率分辯率越高。

一般的分析軟體都是設置譜線數M，採樣點數。信號分析中常用的採樣點數是512、1024、2048、4096等。等效於我們常說的200、400、800、1600線等頻譜線數，頻譜分析一般採樣點數選取2的整數次方。,可見譜線數M越大頻率分辯率△f越小即頻率分辯率越高。

在電機的故障診斷中，為了發現邊帶間隔為極通頻率（一般在以下)的峰值，常常需要極高的分辯率（以下），一般選擇譜線。

至於整周期採樣是很難實現的，必然會因為信號截斷而產生泄露，為了避免這些誤差，所以要採取加窗的辦法。

頻率解析度也可以理解為某一個演演算法（如功率譜估計方法）將原信號中的兩個靠得很近的譜峰依然能保持分開的能力。這是用來比較和檢驗不同演演算法性能好壞的指標。

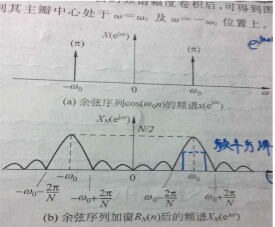
在信號系統中，寬度為的矩形脈衝，它的頻域圖形為函數，兩個一階零點之間的寬度為。由於時域信號的截短相當於時域信號乘了一個形窗函數，那麼該信號的頻域就等同卷積了一個sinc函數，也就是頻域受到函數的調製了，根據卷積的性質，因此兩個信號圓周頻率之差必須大於。

由此可得，如果增加數據點數N，即增加數據長度，也可以使頻率解析度變好，這一點與第一種解釋是一樣的。同時，考慮到窗函數截斷數據的影響存在，當然窗函數的特性也要考慮，在頻率做卷積，如果窗函數的頻譜是個衝擊函數，就相當於沒截斷，可此種情況是不存在的，考慮窗函數主要是以下幾點：

1.主瓣寬度B最小（相當於矩形窗時的，頻域兩個過零點間的寬度）

2.最大邊瓣峰值A最小（這樣旁瓣泄露小，一些高頻分量損失少了）

3.邊瓣譜峰漸近衰減速度D最大（同樣是減少旁瓣泄露）

當今最常見時頻分析方法主要有四種，分別是基於短時傅立葉變換法，基於小波變換法，Choi-Williams分佈法和Hilbert-Huang變換法，經實驗測得Hilbert-Huang具有最高的頻率解析度。

研究數字頻譜最有效方法通常是離散傅里葉變換。

時頻分析是分析時變譜的有力工具，其頻率解析度是值得研究的關鍵問題之一。

通過對基於短時傅里葉變換、小波變換、Choi-Williams分佈和Hilbert-Huang變換的四種時頻分析方法的頻率解析度的實驗比較，說明Hilbert-Huang變換法具有最高的頻率解析度，其次是Choi-Williams分佈，小波緊隨其後，最差是短時傅里葉變換。