半群

群概念的推廣。例如，整數集合對於加法運算是一半群；集合A 的所有子集合組成的集合S(A)對於集合的並，是一半群；集合A上的所有變換T(A)對於變換的乘法，是一半群；集合A 上的所有二元關係R（A）對於關係運算的乘法，是一半群。設 Χ 是一字符集合，是Χ 中的元素組成的有限字元串的集合。若對中的兩個元素、定義二元運算*如下：,則 對於運算*是一半群，並稱之為由Χ 生成的自由半群。

對於半群，廣義結合律成立，即在有限個元素相乘時，不論以什麼樣的方式結合，只要元素排列的次序不變，結果總是相同的。

在半群中，如果對於正整數 n定義，那麼對於正整數m、n有 ,。

若半群中存在元素e，使得對於所有的，都有,則e稱為半群的左單位元素。同樣可定義半群的右單位元素。如果一半群既有左單位元素，又有右單位元素，那麼這兩個元素必是同一個元素；這個元素稱為半群的單位元素。若一半群中存在元素Ζ,使得對於所有的，都有,則Ζ稱為半群的左零元素。同樣可以定義半群的右零元素。如果一半群既有左零元素，又有右零元素，那麼這兩個元素必是同一個元素，並稱之為半群的零元素。若半群中的一個元素x滿足條件 ，則x稱為半群的冪等元素。顯然，單位元素和零元素都是冪等元素。

有單位元素的半群，稱為幺半群。如果給定的一半群S不含單位元素，那麼可以給它補充一個單位元素e,使它成為幺半群其中S的二元運算*已擴展到上，即對所有,恆有，並且。在字符集合Χ上的字元串半群中，可以補上空串，使之成為幺半群。

如果一半群的元素的個數是有限的，那麼這個半群稱為有限半群。任何有限半群S必含有冪等元素，而且對於任何，都有一個形式為的冪等元素。

如果半群S的二元運算是可交換的，即對於，恆有,那麼S稱為可交換半群。在可交換半群中，對於正整數n，有。

如果半群S中存在一個元素α,使得，那麼S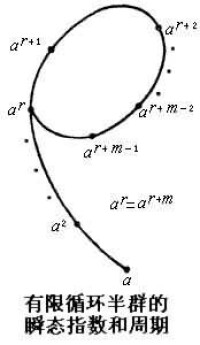所示，這時是S的循環子半群。如果n是m的倍數，滿足，那麼是冪等元素，且是半群的單位元素。如果半群S的一個子集W對於S中規定的二元運算而言仍是一個半群，那麼W稱為S的子半群。

設和是兩個半群,ƒ是從到的一個映射，如果ƒ是保運算的，即對所有的有,那麼ƒ稱為同態映射。當ƒ為滿射時，則稱是的同態像。當ƒ是雙射時，則稱ƒ是同構映射。此時就說半群和是同構的，記為。如果是一個幺半群，含有單位元素,那麼把中映成的那些元素組成的集合稱為同態映射ƒ的核，記為。

如果一半群S有單位元素e且有逆，即對於任何總有元素b使得，那麼半群S是一個群。如果半群S的一個子集A滿足條件,那麼子集A稱為S的左理想。同樣可定義右理想。若A非空且，則稱A是S的真理想。若半群 S無真的左理想，則稱A是左單純的。同樣可定義S是右單純的。

一個半群是群的充分必要條件為：它既無左真理想，又無右真理想。一個有限幺半群是群的充分必要條件為：單位元素是這個半群的惟一冪等元素。

設R是半群S上的一個等價關係，如果對所有的，當時總有，那麼等價關係R稱為右不變的。同樣可定義左不變的等價關係。如果半群 S上的等價關係R既是左不變的，又是右不變的，那麼R稱為S上的合同關係。

設R是半群S上的合同關係，集合S/R是S在關係R之下的等價組集合,是S中和x等價的元素組成的等價組。若把等價組之間的二元運算*定義為，則是一個半群。設MR是如下定義的由S到上的映射:,,,則是一個同態映射。 稱為半群S對於R的商半群。

近年來，半群的理論在計算機科學中得到了應用，引起人們的重視，並成為數學家和計算機科學家深入研究的對象，有了迅速的發展。

參考書目

E. Hille,Functional Analysis and Semigroups, American Mathematical Society, New York,1948.

A.H.Clifford and G.B.Preston,The Algebraic Theory of Semi groups, American Mathematical Society, Pronidence, Rhode Island,1967.

M.A.Arbib,Theories of Abstract Automata, Prentice Hall,Englewood Cliffs, New Jersey, 1969.