約翰遜雜訊

該類型雜訊是由約翰·約翰遜1926年在貝爾實驗室發現並且第一次測量的。他向哈里·奈奎斯特描述了他的發現，奈奎斯特當時也在貝爾實驗室並且能夠解釋這個結果。

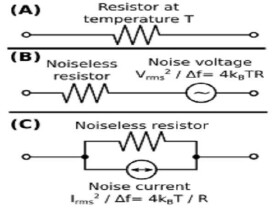
約翰遜雜訊與散粒雜訊完全不同，散粒雜訊包括額外的電流波動，當提供電壓並伴隨宏觀電流開始流動時就會產生。一般情況下，上述定義適用於任何類型的導電介質的電荷載體（例如，電解質中的離子），而不只是電阻。可以通過一個能提供非理想電阻雜訊的電壓源串聯一個無雜訊的理想電阻來模擬。

單邊功率譜密度，或電壓變化（均方）帶寬每赫茲，由下式給出：

其中是玻爾茲曼常數用焦耳每開爾文表示,T是電阻的絕對溫度用開爾文表示，R是電阻值用歐姆(Ω)表示。

該公式可用於室溫下的快速計算：

例如，一個 1 kΩ 電阻溫度在 300 K 時有

對於給定帶寬，電壓 給出

其中 Δf 為已測雜訊之上的帶寬用赫茲表示。一個1 k 電阻器在室溫及 10kHz帶寬情況下的RMS雜訊電壓是400 nV。一個有用的經驗法則需要記住的是，50 Ω 在室溫及 1 Hz 帶寬下對應於 1 nV 的雜訊。

電阻器短路連接時的耗散雜訊功率

電阻器所產生的雜訊可以傳遞至其餘電路；最大的雜訊功率傳遞發生在雜訊產生阻抗與剩餘電路的戴維南等效阻抗阻抗匹配時。在這種情況下兩部分阻抗中的任意一個的耗散雜訊均作用在其本身和其他電阻。由於其中的任何一個電阻只有一半的壓降，因此雜訊功率

此處P是約翰遜雜訊功率用瓦表示。注意這是獨立的雜訊產生阻抗。

雜訊源也可以通過電流源並聯電阻方式來模擬，通過諾頓等效相應的只要簡單地除以R便可以得到。這裡給出該電流源的均方根值為：

約翰遜雜訊是所有電阻的固有屬性，並不是糟糕的設計或製造商的標記，儘管電阻可能還含有多餘的雜訊。

電容器上的約翰遜雜訊被稱為kTC雜訊。約翰遜雜訊在一個RC電路有一個非常簡單的表達，當作阻抗（R）從公式中移除。這是因為更高的R有助於更好的濾波但也產生更多雜訊。RC 電路的雜訊帶寬是 ，它可代入上述公式，以消除R。這樣一個濾波器產生的雜訊電壓的均方與 RMS 為：

約翰遜雜訊在電阻中佔100%的kTC的雜訊。

在極端的情況下開啟一個理想開關會存留“重置雜訊”在電容器上，阻抗是無限的，但公式仍然適用；但是，現在 RMS 必須解釋為非時間上的平均，但是許多這樣的重複事件的平均，由於電壓在帶寬為零時為常數。從這個意義上講，RC電路的約翰遜雜訊可以看作是固有的、電子在電容器上數量分佈熱力學效應，甚至不涉及電阻。

雜訊並非電容器本身引起的，而是由電容器上的一定數量電荷的熱力學波動引起的。一旦電容器與導體電路斷開連接、熱力學波動便“凍結”在如上面給出的一個標準偏差的隨機值上。

電容的複位雜訊感測器通常是一個有限雜訊源，例如在圖象感測器中。作為電壓雜訊的一種替代，電容的複位雜訊也可以進行定量為電荷的標準偏差，有

由於電荷差異是，雜訊常被稱為“KTC 雜訊”。

任何系統在熱平衡有狀態變數與平均能量的 每自由度。使用電容能量()，意味著電容器上的雜訊能量在一個容器中可以看出也為，或. 電容器上的約翰遜雜訊可以從該關係導出，無需考慮阻抗。