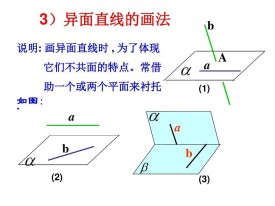
異面直線

不同在任何一個平面內的兩條直線叫做異面直線。空間兩條直線的位置關係有三種，即相交和平行，這兩種情況的兩條直線在同一平面內。另外一種情況就是不相交也不平行稱為異面直線。

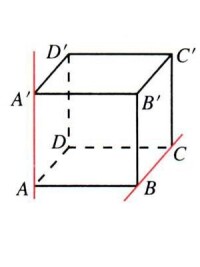
1．分別在兩個平面內的直線是異面直線；

2．在空間不相交的兩條直線是異面直線；

3．平面內的一條直線和平面外的一條直線是異面直線。

既不平行，也不相交。

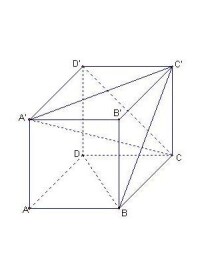
1.兩條異面直線所成的角

直線a、b是異面直線。經過空間任意一點o，分別引直線。直線a'和b'所成的銳角(或直角)叫做異面直線a和b所成的角。兩條異面直線a、b所成角的大小，只由a、b的相互位置來確定，與點o的選擇無關(可以用等角定理來證明)。

2.兩條異面直線的距離

兩條異面直線的公垂線茫這兩條異面直線問的線段的長度，叫做兩條異面直線的距離。

異面直線a、b間的距離，也就是a和過b且平行於a的平面M間的距離。

（1）定義法：由定義判定兩直線永遠不可能在同一平面內

（2）定理：過平面外一點與平面內一點的直線，和平面內不經過該點的直線是異面直線。

例證：

判定定理：平面的一條交線與平面內不經過交點的直線互為異面直線。

已知：。求證：AB和CD互為異面直線。

證明：假設AB和CD在同一平面內，設這個平面是β。即。

由不在同一直線上的三個點確定一個平面可知，α和β重合。

，這與已知條件矛盾。

∴AB和CD不在同一平面內，即AB和CD互為異面直線

兩條異面直線所成的角的定義：直線a，b是異面直線，經過空間一點O，分別引直線,相交直線A，B所成的銳角（或直角）叫做異面直線a,b所成的角。

兩條異面直線垂直的定義：如果兩條異面直線所成的角是直角，則稱這兩條異面直線互相垂直。

兩條異面直線的公垂線的定義：和兩條異面直線都垂直相交的直線叫做兩條異面直線的公垂線。

兩條異面直線的距離的定義：兩條異面直線的公垂線在這兩條異面直線間的線段，叫做這兩條異面直線的公垂線段；公垂線段的長度，叫做兩條異面直線的距離。

3.解析幾何

設兩條空間直線則它們互為異面直線的充要條件是行列式

● ● 和兩條異面直線都垂直相交的直線叫做兩條異面直線的公垂線。

● ● 兩條異面直線的公垂線在這兩條異面直線間的線段，叫做這兩條異面直線的公垂線段，公垂線段的長度，叫做兩條異面直線的距離。

● ● 過平面外一點與平面內一點的直線，和平面內不經過該點的直線是異面直線。

● ● 經過兩條異面直線中的一條，有一個平面與另一條直線平行。

● ● 異面直線的公垂線存在且唯一。

● ● 在兩條異面直線上各任取一點，這兩點形成的所有線段中這兩條異面直線的距離最小。