中心對稱
數學中的概念
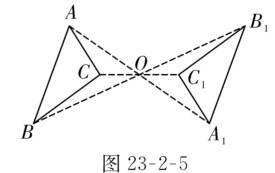
中心對稱是指把一個圖形繞著某一點旋轉180°,如果它能夠與另一個圖形重合,那麼就說這兩個圖形關於這個點對稱或中心對稱(central symmetry)。
中心對稱,是針對兩個圖形而言,是指兩個圖形的(位置)關係。呈中心對稱圖形的對稱點分別在兩個圖形上。
關於中心對稱,有如下特點:
(1)是針對兩個圖形而言。
(2)是指兩個圖形的(位置)關係。
(3)成中心對稱圖形的對稱點分別在兩個圖形上。
也就是說:
● ● 中心對稱圖形:如果把一個圖形繞某一點旋轉180度后能與自身重合,這個圖形是中心對稱圖形。
● ● 中心對稱:如果把一個圖形繞某一點旋轉180度后能與另一個圖形重合,這兩個圖形成中心對稱。
(1)中心對稱的兩個圖形,對稱點所連線段都經過對稱中心.而且被對稱中心平分。
(2)中心對稱的兩個圖形是全等形。
(3)中心對稱的兩個圖形,其對應線段互相平行(或在同一直線上)且相等。
(1)連接原圖形上所有的特殊點和對稱中心。
(2)將以上所連線段延長找對稱點,使得特殊點與對稱中心的距離和對稱點與對稱中心的距離相等。
(3)將對稱點按原圖形的形狀順次連接起來,即可得出關於中心對稱的圖形。
● 一些民間剪紙作品。
● 中心對稱圖形並不只有一個對稱點,比如直線,再比如正弦曲線。
● 既是軸對稱圖形又是中心對稱圖形:直線,線段,兩條相交直線,矩形,菱形,正方形,圓等。
● 中心對稱圖形上每一對對稱點所連成的線段都被對稱中心平分。
● 正三角形不是中心對稱圖形