右手系
在空間中規定直角坐標系的方法之一
右手系(right-hand system)是在空間中規定直角坐標系的方法之一。此坐標系中x軸，y軸和z軸的正方向是如下規定的：把右手放在原點的位置，使大姆指，食指和中指互成直角，把大姆指指向x軸的正方向，食指指向y軸的正方向時，中指所指的方向就是z軸的正方向。也可以按如下方法確定右手(左手)坐標系：如果當右手(左手)的大拇指指向第一個坐標軸(x軸)的正向，而其餘手指以第二個軸(y軸)繞第一軸轉動的方向握緊，就與第三個軸(z軸)重合，就稱此坐標係為右手(左手)坐標系。
定義物體在平面上，即二維的位置時，使用表示兩個方向的坐標軸(稱作笛卡爾坐標或直角坐標)。與此相反，在空間中，即為三維定義位置時，使用的是這3個坐標軸。這是因為平面上的位置用“縱”、“橫”值來表示，對此，三維空間位置則在“縱”、“橫”的基礎上又加上“深”，從而用3個坐標來表示。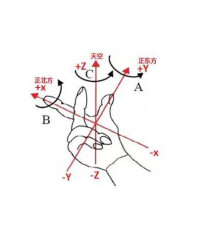
右手系
在三維坐標中，根據軸(深)的不同方向，分為“右手系”和“左手系”兩種坐標系。當軸的方向是（在一般二維直角坐標繫上：向右為軸，向上為軸）從眼前伸向深處時，該坐標系是左手系，反之則是右手系。所謂右手系是用以下方法表示的三維坐標系：
●右手的拇指表示軸
●食指表示軸
●中指表示軸·
也就是把拇指當作軸，食指當作軸，中指當作軸，來考慮三維坐標。如果是右手系，則中指指向自己一方。如果是左手系，則中指指向前方.
解析幾何為了溝通空間圖形與數的研究，需要建立空間的點與有序數組之間的聯繫，為此我們通過引進空間直角坐標系實現。
過定點O，作三條互相垂直的數軸，它們都以O為原點且一般具有相同的長度單位。這三條軸分別叫做x軸(橫軸）、y軸(縱軸)、z軸(豎軸)；統稱坐標軸。通常把x軸和y軸配置在水平面上，而z軸則是鉛垂線；它們的正方向要符合右手規則，即以右手握住z軸，當右手的四指從正向x軸以π/2角度轉向正向y軸時，大拇指的指向就是z軸的正向，這樣的三條坐標軸就組成了一個空間直角坐標系，點O叫做坐標原點。
在徠空間直角坐標系中，讓右手拇指指向x軸的正方向，食指指向y軸的正方向，如果中指能指向z
軸的正方向，則稱這個坐標係為右手直角坐標系．同理左手直角坐標系。
讓左手中指指向x軸的正方向，食指指向y軸的正方向，拇指指向z軸的正方向。
基本信息
- 屬性
- 一個空間直角坐標系
- 中文名
- 右手系
- 相關概念
- 空間直角坐標系，左手系等
- 所屬學科
- 數學（幾何學）
- 全稱
- 右手坐標系
- 外文名
- right-handed system