三維坐標系
三維坐標系
三維笛卡兒坐標系是在二徠維笛卡兒坐標系的基礎上根據右手定則增加第三維坐標(即Z軸)而形成的。同二維坐標系一樣,AutoCAD中的三維坐標系有世界坐標系WCS(World Coordinate System)和用戶坐標系UCS(User Coordinate System)兩種形式。
在三維坐標系中,Z軸的正軸方向是根據右手定則確定的。右手定則也決定三維空間中任一坐標軸的正旋轉方向。
要標註X、Y和Z軸的正軸方向,就將右手背對著屏幕放置,拇指即指向X軸的正方向。伸出食指和中指,如右圖所示,食指指向Y軸的正方向,中指所指示的方向即是Z軸的正方向。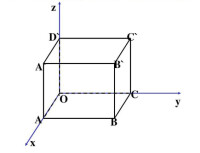

三維坐標系
要確定軸的正旋轉方向,如右圖所示,用右手的大拇指指向軸的正方向,彎曲手指。那麼手指所指示的方向即是軸的正旋轉方向。
2.世界坐標系(WCS)
在AutoCAD中,三維世界坐標系是在二維世界坐標系的基礎上根據右手定則增加Z軸而形成的。同二維世界坐標系一樣,三維世界坐標系是其他三維坐標系的基礎,不能對其重新定義。
3.用戶坐標系(UCS)
用戶坐標係為坐標輸入、操作平面和觀察提供一種可變動的坐標系。定義一個用戶坐標系即改變原點(0,0,0)的位置以及XY平面和Z軸的方向。可在AutoCAD的三維空間中任何位置定位和定向UCS,也可隨時定義、保存和復用多個用戶坐標系。詳見本章第3節。
在AutoCAD中提供了下列三種三維坐標形式:
1.三維笛卡爾坐標
三維笛卡爾坐標(X,Y,Z)與二維笛卡爾坐標(X,Y)相似,即在X和Y值基礎上增加Z值。同樣還可以使用基於當前坐標系原點的絕對坐標值或基於上個輸入點的相對坐標值。
2.圓柱坐標
圓柱坐標與二維極坐標類似,但增加了從所要確定的點到XY平面的距離值。即三維點的圓柱坐標可通過該點與UCS原點連線在XY平面上的投影長度,該投影與X軸夾角、以及該點垂直於XY平面的Z值來確定。例如,坐標“10<60,20”表示某點與原點的連線在XY平面上的投影長度為10個單位,其投影與X軸的夾角為60度,在Z軸上的投影點的Z值為20。
圓柱坐標也有相對的坐標形式,如相對圓柱坐標“@ 10<45 ,30”表示某點與上個輸入點連線在XY平面上的投影長為10個單位,該投影與X軸正方向的夾角為45度且Z軸的距離為30個單位。
3.球面坐標
球面坐標也類似與二維極坐標。在確定某點時,應分別指定該點與當前坐標系原點的距離,二者連線在XY平面上的投影與X軸的角度,以及二者連線與XY平面的角度。例如,坐標“10<45<60”表示一個點,它與當前UCS原點的距離為10個單位,在XY平面的投影與X軸的夾角為45度,該點與XY平面的夾角為60度。
徠同樣,圓柱坐標的相對形式表明了某點與上個輸入點的距離,二者連線在XY平面上的投影與X軸的角度,以及二者連線與XY平面的角度。
註:
1) 在平面直角坐標系中,分別取與x軸、y軸方向相同的兩個單位向量i,j作為一組基底。a為平面直角坐標系內的任意向量,以坐標原點O為起點作向量OP=a。由平面向量基本定理知,有且只有一對實數(x,y),使得 a=向量OP=xi+yj,因此把實數對(x,y)叫做向量a的坐標,記作a=(x,y)。這就是向量a的坐標表示。其中(x,y)就是點P的坐標。向量OP稱為點P的位置向量。
2) 在立體三維坐標系中,分別取與x軸、y軸,z軸方向相同的3個單位向量i,j, k作為一組基底。若a為該坐標系內的任意向量,以坐標原點O為起點作向量OP=a。由空間基本定理知,有且只有一組實數(x,y, z)向量的坐標表示
,使得 a=向量OP=xi+yj+zk,因此把實數對(x,y, z)叫做向量a的坐標,記作a=(x,y, z)。這就是向量a的坐標表示。其中(x,y, z),也就是點P的坐標。向量OP稱為點P的位置向量。
三維笛卡爾坐標(X,Y,Z)是在三維笛卡爾坐標系下的點的表達式,其中,x,y,z分別是擁有共同的零點且彼此相互正交的x軸,y軸,z軸的坐標值。
圓柱坐標(ρ,θ,z)是圓柱坐標繫上的點的表達式。設P(x,y,z)為空間內一點,則點P也可用這樣三個有次序的數ρ,θ,z來確定,其中ρ為點P在xoy平面的投影M與原點的距離,θ為有向線段PO在xoy平面的投影MO與x軸正向所夾的角。圓柱坐標系和三維笛卡爾坐標系的點的坐標的對應關係是,x=ρcosθ,y=ρsinθ,z=z。
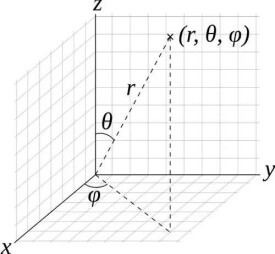
球面坐標系由到原點的距離、方位角、仰角三個維度構成。球面坐標(ρ,θ,φ)是球面坐標繫上的點的表達式。設P(x,y,z)為空間內一點,則點P也可用這樣三個有次序的數r,φ,θ來確定,其中r為原點O與點P間的距離,θ為有向線段與z軸正向所夾的角,φ為從正z軸來看自x軸按逆時針方向轉到有向線段的角,這裡M為點P在xOy面上的投影。這樣的三個數r,φ,θ叫做點P的球面坐標,這裡r,φ,θ的變化範圍為 r∈[0,+∞), φ∈[0, 2π], θ∈[0, π] . r = 常數,即以原點為心的球面; θ= 常數,即以原點為頂點、z軸為軸的圓錐面; φ= 常數,即過z軸的半平面。其中 x=rsinθcosφ y=rsinθsinφ z=rcosθ