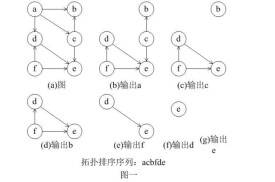
拓撲排序
拓撲排序
對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序,是將G中所有頂點排成一個線性序列,使得圖中任意一對頂點u和v,若邊(u,v)∈E(G),則u在線性序列中出現在v之前。通常,這樣的線性序列稱為滿足拓撲次序(Topological Order)的序列,簡稱拓撲序列。簡單的說,由某個集合上的一個偏序得到該集合上的一個全序,這個操作稱之為拓撲排序。
較程划程,程稱活動(activity)。在整個工程中,有些子工程(活動)必須在其它有關子工程完成之後才能開始,也就是說,一個子工程的開始是以它的所有前序子工程的結束為先決條件的,但有些子工程沒有先決條件,可以安排在任何時間開始。為了形象地反映出整個工程中各個子工程(活動)之間的先後關係,可用一個有向圖來表示,圖中的頂點代表活動(子工程),圖中的有向邊代表活動的先後關係,即有向邊的起點的活動是終點活動的前序活動,只有當起點活動完成之後,其終點活動才能進行。通常,我們把這種頂點表示活動、邊表示活動間先後關係的有向圖稱做頂點活動網(Activity On Vertex network),簡稱 AOV網。
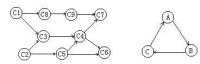
圖3-5 這種先後關係的AOV網
例,假計算專業必須完圖-列課程。,課程,習課程示項,習課程決件完修課程。習《據構》課程必須排完修課程《離散》《算語言》。習《》課程則隨排,基礎課程,修課。若網示課程排系,則圖-示。圖頂課程,課程終課程修課。圖清楚各課程修續系。課程修課,續課程。
網該環圖,即該,若,則。圖-具頂,必須,必須,推必,必須,矛盾,項。況若程序,則稱死鎖或死循環,是應該必須避免的。
在AOV網中,若不存在迴路,則所有活動可排列成一個線性序列,使得每個活動的所有前驅活動都排在該活動的前面,我們把此序列叫做拓撲序列(Topological order),由AOV網構造拓撲序列的過程叫做拓撲排序(Topological sort)。AOV網的拓撲序列不是唯一的,滿足上述定義的任一線性序列都稱作它的拓撲序列。
由AOV網構造出拓撲序列的實際意義是:如果按照拓撲序列中的頂點次序,在開始每一項活動時,能夠保證它的所有前驅活動都已完成,從而使整個工程順序進行,不會出現衝突的情況。
由AOV網構造拓撲序列的拓撲排序演演算法主要是循環執行以下兩步,直到不存在入度為0的頂點為止。
(1)選擇一個入度為0的頂點並輸出之;
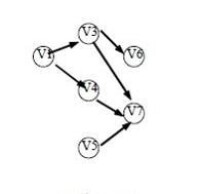
拓撲排序
循環結束后,若輸出的頂點數小於網中的頂點數,則輸出“有迴路”信息,否則輸出的頂點序列就是一種拓撲序列。
拓撲排序常用來確定一個依賴關係集中,事物發生的順序。例如,在日常工作中,可能會將項目拆分成A、B、C、D四個子部分來完成,但A依賴於B和D,C依賴於D。為了計算這個項目進行的順序,可對這個關係集進行拓撲排序,得出一個線性的序列,則排在前面的任務就是需要先完成的任務。
注意:這裡得到的排序並不是唯一的!就好像你早上穿衣服可以先穿上衣也可以先穿褲子,只要裡面的衣服在外面的衣服之前穿就行。
拓撲序列Pascal代碼(無優化)
拓撲序列C++(STL)核心代碼
這裡的代碼可以參考這本書,這裡是我自己敲的代碼,用了容器,感覺能看明白點。
拓撲序列Pascal代碼(鄰接表+隊列優化)
這裡主要是將入度為零的點加入隊列stack,直接在隊列內擴展即可,效率為O(n+m)