相互擴散

蘇聯科學家首先用凝聚物體相互作用的擴散理論解釋聚合物對固體表面的膠接現象。這個理論起初是作為聚合物自粘的理論而發展起來的，后擴展到聚合物的膠接。

依照擴散理論，膠擦與自粘現象均是由於聚合物高分子的端頭或鏈節穿過最初接觸面的擴散形成的。因為膠粘劑一般處於液體狀態，膠粘劑高分子比被膠接材料的分子更易運動，所以膠接基本上是由於膠粘劑高分子的擴散所造成的。當被膠接物在溶劑中具有溶脹能力時，同樣也存在被膠接物分子向膠粘劑內那的擴散，從擴散理論的觀點看，膠接和自粘現象是空間現象，而不是表面現象。這樣，膠接接頭強度特性的分析屬於高聚物強度的範疇。

一種物質分子在另一種物質分子中的擴散不是別的，正是物質的溶解過程，根據聚合物的膠接能力可以確定它們的相容性，或者根據它們的相容性確定聚合物的膠接能力。因為聚合物和其它材料的互溶度由它們的極性關係所確定，那麼為了獲得牢固的接頭，聚合物間必需的互溶性原理與實驗法則相吻合，根據該法則極性物質與非極性物質間不能形成牢固的膠接接頭。

擴散理論的要證明是膠接接頭強度對膠粘劑與被膠接物接觸時間長短的依賴性和對接頭強度形成時對溫度的依賴性，

以及對聚合物分子量的依賴關係。同樣，還有聚合物最初接觸界面消失的特性。然而必須指出，在聚合物之間最初接觸界面的消失不能看作為高分子擴散的唯一證明。

不容置疑，聚合物的自粘和膠接時擴散起著巨大的作用。然而，很難肯定在聚合物與金屬接觸時大分子鏈節或大分子的擴散具有任何實質的意義，儘管與聚合物的自粘和膠接現象一樣，在許多情況下其膠接接頭強度與接觸時間、製備溫度和聚合物分子量相關。

在粉末冶金工藝中，控制均勻化動力學的參數是顆粒尺寸，燒結時間和燒結溫度。顆粒尺寸是很重要的，因為均勻化直接與擴散距離的平方有關。粉末顆粒尺寸決定了擴散距離，並且起著十分重要的作用。如果壓坯是由兩種粉末的混合料製成的，微量組元粉末的顆粒尺寸在確定擴散距離方面是更加重要。因為微量組元粉末是分佈在主要組元粉末的基體上，這個基體或多或少是連續的。組成物的分佈儘可能接近理想的統計分佈，就可促使快速均勻化。這就意味著粉末組成物要相互混合得很好。高的壓坯密度，意味採用高的壓制壓力，可以使粉末顆粒間接觸得更緊密，而在這些粉末顆粒之間是要發生相互擴散的，所以這樣就可加快均勻化的速率。然而，在低溫進行均勻化處理時，表面擴散可能起著重要的作用，因此有更多的內表面而不太緻密的壓坯可能是有利的。

溫度影響均勻化速度，因為溫度與混合料組成物間的擴散係數D有關，它可以寫成： ，式中D是與溫度無關的常數，Q是擴散激活能，R是氣體常數，T是絕對溫度。這意味著擴散係數隨溫度快速增加。在通常的燒結溫度下擴散係數是足夠大的，以至具有通常顆粒尺寸大小分佈的粉末混合料，可以在一般工業用的燒結時間內得到完全均勻化。例如做結構零件的鐵與石墨的混合料，在1100℃，碳向奧氏體中的擴散係數為7x10m/s。而另一方面，當需要用鐵和鎳或錳的元素粉末混合料來生產均勻的鐵鎳或鐵錳合金時，就需要很細的粉末或者是很長的燒結時間和很高的燒結溫度。在1100℃鐵向鎳中的擴散係數為8x10m/s。在相同溫度下比碳向奧氏體中的擴散係數低10倍。如果希望由粉末製取一種成分上完全均勻化的合金鋼，可以用一種含有金屬合金元素但沒有碳的預合金粉末與石墨相混合，經過壓制和燒結而製得。雖然，合金粉末與石墨粉末的混合料的壓制性要低於元素粉末混合料的。

這並不意味著在用金屬粉末混合料製取材料時總是需要完全均勻化。部分均勻化合金材料的性能研究才剛剛開始。一種部份預合金化粉末與石墨粉相混合，而後進行通常的壓制和燒結。這種部分預合金化粉末是採用擴散粘結工藝製成的，即將工業用鎳、銅和鉬粉通過擴散與工業用鐵粉粘結在一起。只要將部分均勻化合金進行熱處理，就可得到可以應用於結構零件的極好的機械性能。

在由鐵粉和合金元素粉末，如鉻、硅和鉬，混合料製成的壓坯中，其均勻化的速率均比鐵鎳或鐵錳合金粉混合料的快。鐵粉和合金元素粉末如鉻，硅和鉬混合料的成分是在鐵素體區，在相應的二元相圖中γ區環的外面。快速均勻化的原因在於鐵與鉻、硅和鉬形成的固溶體的晶體結構是體心立方。在鐵素體合金中鐵與合金元素間的擴散係數要比鐵和合金元素在奧氏體固溶體合金中的擴散係數約大100倍。在燒結溫度通過互相擴散形成鐵素體合金的一個實際的例子，是用於磁性材料的鐵硅合金。把鐵粉和鐵硅粉末混合進行壓制，在接近1300℃燒結一小時，可以製成含3%硅的合金。它具有均勻的顯微組織和令人滿意的磁學性能。

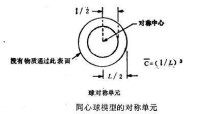
金屬粉末混合料壓坯在燒結過程中的均勻化首先由Rhines進行了半定量的研究。Rudmen和其合作者採用了更加定量的方法。Heckel和他的同事對金屬粉末顆粒間的相互擴散的模型進行了研究和比較，並且使得今天對這個領域的了解或多或少達到明了的階段。本處中對於相互擴散的定量分析只列舉一個例子，這還不是完美無缺的處理，並且要省略大量的數學推導。這個例子是與二元系金屬粉末混合料壓坯中相互擴散有關，在壓坯中可以形成一系列完全相互溶解的固溶體，如銅和鎳。這個模型可以叫做同心球擴散模型。這種模型包含有一個混合料中微量組元球，例如鎳，其直徑為l，可代表是鎳的顆粒尺寸。這個鎳球鑲嵌在主要組元球，例如銅裡面。銅球的直徑為L。它等於鎳球直徑除以合金平均成份的3次方根： ，對於含有20%體積鎳粉的鋼鎳混合料，如果鎳粉球的直徑為100μm，則銅粉球的直徑將是。球型的球對稱單元表示如圖。對於這一簡單的球殼模型，在不穩態擴散時Fick方程的解已經求出來了，而後應用到整個壓坯中的物質擴散。這個解是很複雜的，並且包含有數值方法和計算機技術。

當兩種材料緊密結合時，一種材料的分子會通過擴散轉移到另外一種材料中去，材料原子的運動也能引發此類現象。從原子的觀點來看，擴散是晶格節點處的原子遷移現象。原子必須擁有足以破壞現有節點的能量，才能在另外的品格處形成新的節點。擴散速度是一種典型的材料特徵，它可以通過實驗度量獲得。擴散過程的最常見數學描述是Fick第二定律：

其中，C是擴散物種的濃度，是梯度運算元空間，t是時間，D是擴散係數。可以通過明確定義的實驗室試驗描述D的值，大部分工程材料的擴散係數可以從材料手冊中查得。

擴散現象本身不是一種失效機理，例如對於擴散粘合來說，它還是有益的機制。然而，當擴散介質是有害物質或是化學腐蝕品，那麼它就表現為一種失效動因；另外，當擴散導致微觀結構的老化、有害的蠕變變形、金屬的遷移和不平衡的相互擴散等現象時，它也是一種失效動因。

當兩種材料必須相互粘合時，相互擴散現象對於形成接觸面粘合力是非常重要的。然而，如果兩種材料的有效擴散速度不相等，其中一種材料就會耗盡其原子，從而引發可肯達爾效應，並損失接觸面處的強度。常見的例子是電子設備絲焊點處金浸出到鋁中引起紫斑（Au-Al合金加熱缺陷）。兩種粘合材料的互擴散常數一定要相近，這樣才能避免此類失效機理。換句話說，某段時間內，由溫度協助的過度擴散會使界面處出現金屬化合物的增加，進而導致脆性界面韌性不足。

相互擴散是一種與時間相關的現象，因此，它是一種磨損機理。

晶體的表面與體內的結構有很大的不同，晶體中原子排列的三維周期性在表面處突然中斷，如圖顯示的是晶體表面處的電勢能。特殊的表面特性使得兩種材料的界面處產生了很多值得研究的有趣現象。

薄膜製備時。一般都使薄膜生長在某一襯底上，因而在薄膜與襯底之間就存在一個界面。界面處的晶格結構或由薄膜和襯底兩種不同物質在製備過程中發生的界面化學反應，對薄膜的緻密度、力學、熱學和電學等性能都會造成影響。另外，隨著對薄膜研究和應用的深入，人們發現多層膜比單層膜具備更多、更好的性能，因此經常需要製備多層結構的薄膜，即在同一襯底沉積兩層以上的不同或相同厚度的薄膜。多層膜問的界面處容易存在雜質和缺陷，並且由於兩種材料之間存在原子的交換作用和擴散現象，對薄膜的性能產生巨大的影響，因此對不同材料界面的研究也是非常必要的。