夫琅禾費衍射

光源和觀察幕離障礙物（孔或屏）均為無窮遠的衍射現象。實驗裝置如圖，S為單色點光源，放置在透鏡L1的物方焦點處，所得平行光垂直入射到障礙物，藉助於透鏡L2將無窮遠處的衍射圖樣移至L2的像方焦面上觀察。

根據惠更斯-菲涅耳原理，單縫後面空間任一點P的光振動是單縫處波陣面上所有子波波源發出的子波傳到P點的振動的相干疊加。

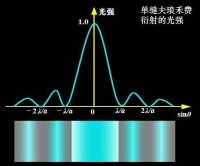
單縫衍射障礙物為單狹縫，其長度比縫寬a要大得多，故可看作無窮長。由於在縫的長度方向對入射光沒有限制，在該方向上不發生衍射；在垂直於縫長方向對光有限制，將發生衍射。幕上P點的強度I取決於衍射角為θ的衍射光在該點的相干疊加結果，圖中為其強度分佈曲線，I0為中心點O的光強。時，，強度達極大值，稱衍射主極大（或中央極大）。當衍射角θ滿足時，，稱衍射極小。相鄰兩極小間有一次極大，其強度遠比中央極大要小，中央極大佔有入射能量的絕大部分。

當縫寬aλ時，所有次極大和極小均向中心點O靠攏，在極限情形下縮成一點，此即幾何光學的結果。只有當縫寬a與波長λ可比擬時才能觀察到明顯的衍射現象。衍射極小（或極大）的位置和間距與波長有關，對不同波長的光，除中央極大重合外，其他各級次極大均彼此分離，所以，用白光作為光源時將會得到彩色衍射圖樣。

圓孔的夫琅禾費衍射為用一個小孔來代替狹縫，當平行單色光垂直照射在圓孔上時，在透鏡上的焦平面就可以觀察到圓孔的夫琅禾費衍射花樣。中間是一較亮的圓斑，外圍是一組同心的明環和暗環，以第一暗環為邊界的中央亮斑約佔整個入射光線光強的84%，我們把這個中央亮斑叫做艾里斑（Airy disk).

在標量衍射理論中，夫琅禾費近似是對菲涅耳衍射積分的遠場近似式。

解釋

夫琅禾費衍射使用惠更斯－菲涅耳原理，藉以把通過圓孔或狹縫的一波動分成多個向外的波動，使用透鏡來有目的地衍射光的觀測實驗一般被用作描述這個原理。當波動通過時，波動會被衍射分成兩個波動，之後以平行的角度各自行進，後面跟著進來的波動亦是如此，在觀測時把屏幕放在行進路線上來看成像條紋這個方法就用到這樣的原理。

當一遭到衍射的波動在最初衍射點的近場距離，在與其他波動平行下被觀測到時，我們會看到菲涅耳衍射，因為用圓孔與屏幕間距離用菲涅耳數方程計算出的結果小於1，這方程可在觀測平行波的衍射程度時用到，方程需要的物理量為圓孔或縫隙的大小、波長以及離圓孔的距離。當距離或波長增加時，由於在圓孔或物件邊緣的波動開始變得像平面波，所以會產生夫琅禾費衍射。

圓孔形式

觀測時，會看到菲涅耳衍射所產生的圓孔成像，大小與形狀會與原來的圓孔不一樣，即是說邊緣多少會有一些鋸齒在，但是夫琅禾費衍射的成像則只有大小的改變，這是因為遠場的波動比較接近平行光束及平面波的性質。

遠場衍射條紋可在校準好的透鏡的成像平面上被觀測到（大小除外）。點狀光源在衍射屏產生的遠場條紋可在光源的成像平面上被觀測到。

假如一光源與觀察用的屏幕離衍射圓孔（可以是狹縫）足夠遠的話，到達圓孔及屏幕的波前可被視為準直或平面波。菲涅耳衍射（或近場衍射）只會在上述情況不被滿足時發生，而這時就需要考慮到入射波前的弧度。

在遠場衍射中，如果觀測屏幕在圓孔不動時往後移動，則產生的條紋會一致地改變大小。但近場衍射則不會這樣，衍射條紋的大小與影狀都會改變。

狹縫形式

要做到夫琅禾費狹縫衍射，可以使用兩塊透鏡及一片屏幕。使用點狀光源及准直透鏡可以做出平行光束，然後這光束會通過狹縫。狹縫後會有另一塊透鏡，把平行光束聚焦到屏幕上作觀測之用。同樣的設置可用於多狹縫衍射，會造出不同的衍射條紋。

由於這種衍射數學上並不複雜，實驗設置可以很準確地找出入射單色光的波長。