零矩陣
零矩陣
零矩陣,在數學中,特別是在線性代數中,零矩陣即所有元素皆為0的矩陣。
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。
在線性代數中,對於n階方陣N,存在正整數k,使得N^k=0,這樣的方陣N就叫做冪零矩陣。滿足條件的最小的正整數k被稱為N的度數或指數。
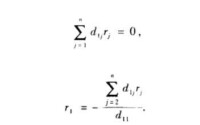
零矩陣
Matlab中用zeros函數產生一個零矩陣,zeros函數的使用規則:>> zeros(n)即產生一個 n*n 的零矩陣。
如:
>>zeros(5)
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
* m×n 的零矩陣 O 和 m×n 的任意矩陣 A 的和為 A + O = O + A = A ,差為 A - O = A,O - A = -A。
* l×m 的零矩陣 O 和 m×n 的任意矩陣 A 的積 OA 為 l×n 的零矩陣。
* l×m 的任意矩陣 B 和 m×n 的零矩陣 O 的積 BO 為 l×n 的零矩陣。
