線面平行
直線與平面無公共點
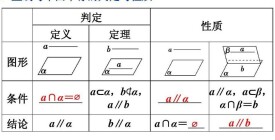
定義:一條直線與一個平面無公共點(不相交),稱為直線與平面平行。
一條直線與一個平面無公共點(不相交),稱為直線與平面平行。
平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行。
線面平行
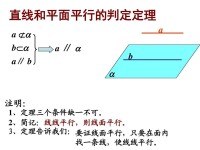
反證法證明:假設a與α不平行,則它們相交,設交點為A,那麼
∵,∴A不在b上
在α內過A作,則
又∵,與矛盾。
∴假設不成立,
向量法證明:設a的方向向量為a,b的方向向量為b,面α的法向量為p。
∵
∴,
∵,由共線向量基本定理可知存在一實數k使得
那麼
即
∴
平面外一條直線與此平面的垂線垂直,則這條直線與此平面平行。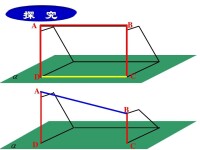 已知:,且a不在α上。求證:證明:設a與b的垂足為A,b與α的垂足為B。假設a與α不平行,那麼它們相交,設,連接BC由於不在直線上的三個點確定一個平面,因此ABC首尾相連得到,即,即∴在中,有兩個內角為90°,這是不可能的事情。∴假設不成立,
已知:,且a不在α上。求證:證明:設a與b的垂足為A,b與α的垂足為B。假設a與α不平行,那麼它們相交,設,連接BC由於不在直線上的三個點確定一個平面,因此ABC首尾相連得到,即,即∴在中,有兩個內角為90°,這是不可能的事情。∴假設不成立,

線面平行
(1)利用定義:證明直線與平面無公共點;
(2)利用判定定理:從直線與直線平行得到直線與平面平行;
(3)利用面面平行的性質:兩個平面平行,則一個平面內的直線必平行於另一個平面。
註:線面平行通常採用構造平行四邊形來求證。
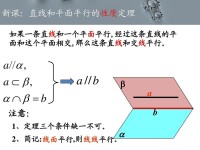
一條直線和一個平面平行,則過這條直線的任一平面與此平面的交線與該直線平行。
線面平行
證明:假設a與b不平行,設它們的交點為P,即P在直線a,b上。
∵
與矛盾
∴
此定理揭示了直線與平面平行中蘊含著直線與直線平行。通過直線與平面平行可得到直線與直線平行。這給出了一種作平行線的重要方法。
注意:直線與平面平行,不代表與這個平面所有的直線都平行,但直線與平面垂直,那麼這條直線與這個平面內的所有直線都垂直。
一條直線與一個平面平行,則該直線垂直於此平面的垂線。
已知:。求證: 證明:由於α的垂線有無數條,因此可將b平移至與a相交,設平移的直線為c,,c與α的垂足為N。∵兩條相交直線確定一個平面∴設a和c構成的平面為β,且,且由定理1可知由於平移不改變直線的方向,因此
證明:由於α的垂線有無數條,因此可將b平移至與a相交,設平移的直線為c,,c與α的垂足為N。∵兩條相交直線確定一個平面∴設a和c構成的平面為β,且,且由定理1可知由於平移不改變直線的方向,因此

線面平行