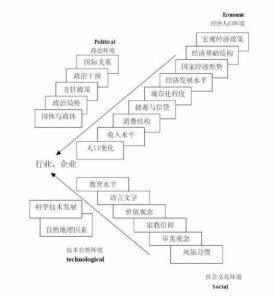
趨勢分析法
趨勢分析法
趨勢分析法是通過對有關指標的各期對基期的變化趨勢的分析,從中發現問題,為追索和檢查帳目提供線索的一種分析方法。例如通過對應收帳款的趨勢分析,就可對壞帳的可能與應催收的貨款作出一般評價。趨勢分析法可用相對數也可用絕對數。
通過趨勢分析可以知道企業財務經營的變化情況,為預測未來發展方向提供幫助。
確定引起公司財務狀況和經營成果變動的主要原因;
確定公司財務狀況和經營成果的發展趨勢對投資者是否有利;預測公司未來發展的趨勢。這種分析方法屬於一種動態分析,它是以差額分析法和比率分析法為基礎,同時又能有效地彌補其不足。
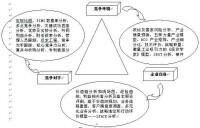
趨勢分析法
1、定基動態比率:即用某一時期的數值作為固定的基期指標數值,將其他的各期數值與其對比來分析。其計算公式為:定基動態比率=分析期數值÷固定基期數值。例如:以2000年為固定基期,分析2001年、2002年利潤增長比率,假設某企業2000年的凈利潤為100萬元,2001年的凈利潤為120萬元,2002年的凈利潤為150萬元。則:
2001年的定基動態比率=120÷100=120%
2002年的定基動態比率=150÷100=150%
2、環比動態比率:它是以每一分析期的前期數值為基期數值而計算出來的動態比率,其計算公式為:環比動態比率=分析期數值÷前期數值。仍以上例資料舉例,則:
2001年的環比動態比率=120÷100=120%
2002年的環比動態比率=150÷120=125%
趨勢分析法
例如:某企業利潤表中反映2000年的凈利潤為50萬元,2001年的凈利潤為100萬元,2002年的凈利潤為160萬元。
通過絕對值分析:2001年較2000年相比,凈利潤增長了100-50=50(萬元);2002年較2001年相比,凈利潤增長了160-100=60(萬元),說明2002年的效益增長好於2001年。
而通過相對值分析:2001年較2000年相比凈利潤增長率為:(100-50)÷50×100%=100%;2002年較2001年相比凈利潤增長率為:(160-100)÷100×100%=60%。則說明2002年的效益增長明顯不及2001年。
趨勢分析法
在採用趨勢分析法時,必須注意以下問題:1、用於進行對比的各個時期的指標,在計算口徑上必須一致;2、必須剔除偶發性項目的影響,使作為分析的數據能反映正常的經營狀況;3、應用例外原則,對某項有顯著變動的指標作重點分析,研究其產生的原因,以便採取對策,趨利避害。
趨勢分析法總體上分四大類:(一)縱向分析法;(二)橫向分析法;(三)標準分析法;(四)綜合分析法。此外,趨勢分析法還有一種趨勢預測分析。
趨勢預測分析運用回歸分析法、指數平滑法等方法來對財務報表的數據進行分析預測,分析其發展趨勢,並預測出可能的發展結果。以下先簡要介紹如何運用趨勢線性方程來作趨勢預測分析,其它四類方法後面分別介紹。
趨勢線性方程是作趨勢分析時,預測銷售和收益所普遍採用的一種方法。公式表示為:y=a+bx
其中:a和b為常數,x表示時期係數的值,x是由分配確定,並要使∑x=0。為了使∑x=0。當時期數為偶數或奇數時,值的分配稍有不同。
趨勢分析(TrendAnalysis)最初由Trigg's提出,採用Trigg's軌跡信號(Trigg'sTracking Signal)對測定方法的誤差進行監控。此種軌跡信號可反映系統誤差和隨機誤差的共同作用,但不能對此二者分別進行監控。其後,Cembrowski等單獨處理軌跡信號中的兩個估計值,使之可對系統誤差和隨機誤差分別進行監控,其—即為“準確度趨勢”(均數)指示系統—Trigg's平均數規則,其二即為反映隨機誤差的“精密度趨勢”(標準差)指示系統—Trigg's方差卡方規則。趨勢分析與傳統的Shewhart控制圖在表面上有類似之處,即用平均數來監測系統誤差.而用極差或標準差來監測隨機誤差。然而,在趨勢分析中,平均數(準確度趨勢)和標準差(精密度趨勢)的估計值是通過指數修勻(exponential smoothing)方法獲得的。指數修勻要引入權數來完成計算,而測定序列的每一次測定中,后一次測定的權數較前一次為大,因此增加了對剛剛開始趨勢的響應,起到了“預警”和“防微杜漸”的作用。
趨勢分析法
通過指數修勻獲得的平均值估計值稱為修勻平均數(sm—mean)。在測定序列中每一次測定的sm—mean,由公式9—1進行計算:sm—mean=a×(新的一次控制測定值)+(1—a)×(前sm—mean) (9—1)式中a是修勻係數,由控制測定值個數(N)決定,a=2/(N+1),(0 此規則主要用於監測系統誤差,即是趨勢分析中“準確度趨勢分析”指示系 統。在應用此規則時,最初開始計算修勻平均數(sm—mean)的“前sm—mean’,實際上即為質控物測定值的平均數(T—mean)。若最初質控物的標準差為Ts,則用此平均數規則評價質控狀態時,系由質控物的平均數檢驗修勻平均數的估計值,而以Z-值進行檢驗:
此規則主要用於監測系統誤差,即是趨勢分析中“準確度趨勢分析”指示系 統。在應用此規則時,最初開始計算修勻平均數(sm—mean)的“前sm—mean’,實際上即為質控物測定值的平均數(T—mean)。若最初質控物的標準差為Ts,則用此平均數規則評價質控狀態時,系由質控物的平均數檢驗修勻平均數的估計值,而以Z-值進行檢驗: (Pfr=0.05;Pfr=0.01,Pfr=0.002) 此規則主要用於監測隨機誤差,即趨勢分析中“精密度趨勢分析”指示系統;其中最關鍵的統計量為修勻標準差sm—s,sm—s的數學表達式為:
(Pfr=0.05;Pfr=0.01,Pfr=0.002) 此規則主要用於監測隨機誤差,即趨勢分析中“精密度趨勢分析”指示系統;其中最關鍵的統計量為修勻標準差sm—s,sm—s的數學表達式為:
 算數平均法適用於每月銷售量波動不大的產品的銷售預測 加權平均法中的權數選取應該遵循“近大遠小”的原則
算數平均法適用於每月銷售量波動不大的產品的銷售預測 加權平均法中的權數選取應該遵循“近大遠小”的原則
由上述計算公式可知,最近的控制測定值由a加權,倒數第二個最近控制測定值由a(1—a)加權,倒數第三個最近控制測定值由。a(1—a)2加權,等等。若a為0.2,則最近的控制測定值的權數為0.2,按逆順序,前面的控制測定值的權數依次為0.16,0.128等等。
對於標準差可進行類似的計算,但其計算更加複雜,因為必須首先計算新的控制測定值與平均數估計值之間的差,而該差值則被稱為預測誤差。
預測誤差=新的控制測定值一前sm—mean (9—2)
修勻預測誤差(SFE)=a×(新的預測誤差)十(1—a)×(前修勻預測誤差) (9—3)
預測誤差通過指數修勻計算處理得出精密度估計值,稱為平均絕對偏差(MAD,Mean Absolute Deviation)。
MAD=a×(新的預測誤差)—(1—a)×(前MAD) (9—4)
最後可得:
軌跡信號=修勻預測誤差(SFE)/平均絕對偏差(MAD)) (9—5)
一般把軌跡信號在95%和99%可信水平定為警告和失控的界限(見表9—3)。
表9—3 不同N時軌跡信號的控制限
N a 警告界限 失控界限
5 0.33 0.71 0.82
10 0.20 0.61 0.80
15 0.10 0.41 0.54
20 0.10 0.41 0.54
(Pfr=0.01。Pfr=0.002)

趨勢分析法
Z=N(sm—mean—T—mean)/Ts (9—6)
其中Z相當於標準差的個數,與統計檢驗“顯著性水平”有關。由Pfr確定的不同水平的Z值,即可根據公式9—6計算出Trigg's平均數規則中修勻平均數(sm—nlean)的控制限(見表9—4)。
表9—4 Trigg's平均數規則的控制限
N a 控制限
Pfr=0.01 Pfr=0.002
5 0.33 1.25(Ts) 1.38(Ts)
10 0.20 0.82(Ts) 0.98(Ts)
15 0.10 0.67(Ts) 0.79(Ts)
20 0.10 0.58(Ts) 0.69(Ts)

趨勢分析法
修勻標準差 (9—7)
式中的a和MAD在上面已定義。具體方法是:由卡方(X2)統計檢驗對修勻標準差(sm—s)估計值的顯著性變化進行檢驗,即將“真”方差(T2s)與修勻標準差的平方(sm2s)進行比較:
X2=(sm2s/T2s)×(N-1) (9—8)
由Pfr確定在不同水平的臨界卡方值(X2)並根據公式9—8計算的Trigg's方差卡方規則的控制限-見表9—5。
表9—5 Trigg's方差卡方規則的控制限
N a 控制限
Pfr=0.05 Pfr=0.01 Pfr=0.002
5 0.33 1.54(Ts) 1.82(Ts) 2.15(Ts)
10 0.20 1.37(Ts) 1.55(Ts) 1.75(Ts)
15 0.10 1.30(Ts) 1.44(Ts) 1.61(Ts)
20 0.10 1.26(Ts) 1.38(Ts) 1.52(Ts)

趨勢分析法
移動平均法適用於銷售量略有波動的產品預測
指數平滑法實質上是一種加權平均法
目錄