外角
兩條邊延長線組成的角
三角形內角和等於180度；一個外角大於與它不相鄰的任一個內角，等於與它不相鄰的兩個內角和，多邊形的外角和為360度，外角越多，越接近圓。多邊形的一條邊與另一條邊的延長線組成的角，叫做多邊形的 外角。
圓外角的相關定理：圓外角的度數等於圓外角所對的長弧的度數與短弧的度數的差的一半.
多邊形的一條邊與另一條邊的延長線組成的角，叫做多邊形的外角。
N邊形內部連接對角線可分成個三角形，內角和是度，延長N邊形的N條邊，外角和度。
註：在不考慮角度方向的情況下，以上所述的N邊形，僅為任意‘凸’多邊形。當考慮角度方向的時候，上面的論述也適合凹多邊形。
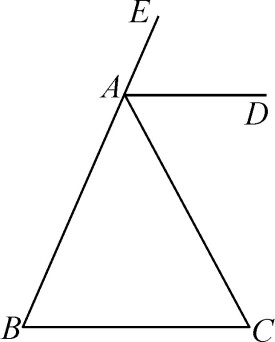
三角形的一條邊的延長線和另一條相鄰的邊組成的角，叫做三角形的外角。
角形的外角性質
三角形的外角具有以下性質：
①頂點是三角形的一個頂點，一邊是三角形的一邊，另一邊是三角形的一邊的延長線。
②三角形的一個外角等於與它不相鄰的兩個內角和。
③三角形的一個外角大於與它不相鄰的任何一個內角。
④三角形的外角和是360° 三角形內角是兩條線段的夾角 三角形的內角和為180度；三角形的一個外角等於另外兩個內角的和；三角形的一個外角大於其他兩內角的任一個角。
圓內角的相關定理：圓心角所對的弧的度數等於弧所對的圓心角的度數；圓周角的度數等於圓心角的度數的一半;
圓外角的相關定理：圓外角的度數等於圓外角所對的長弧的度數與短弧的度數的差的一半.
三角形有6個外角，四邊形有8個外角，外角的個數等於多邊形的邊數乘以2，三角形6個外角之和是720°。
基本信息
- 中文名
- 外角
- 外文名
- exterior angle
- 應用領域
- 數理科學
- 定義
- 一條邊與另一條邊的延長線組成角
- 性質
- 外角和都等於360度
- 特點
- 外角越多，越接近圓