Boosting
提高給定學習演演算法準確度的方法
提升方法(Boosting),是一種可以用來減小監督式學習中偏差的機器學習演演算法。面對的問題是邁可·肯斯(Michael Kearns)提出的:一組“弱學習者”的集合能否生成一個“強學習者”?弱學習者一般是指一個分類器,它的結果只比隨機分類好一點點;強學習者指分類器的結果非常接近真值。
Boosting是一種提高任意給定學習演演算法準確度的方法。它的思想起源於 Valiant提出的 PAC ( Probably Approximately Correct)學習模型。Valiant和 Kearns提出了弱學習和強學習的概念 ,識別錯誤率小於1/2,也即準確率僅比隨機猜測略高的學習演演算法稱為弱學習演演算法;識別準確率很高並能在多項式時間內完成的學習演演算法稱為強學習演演算法。同時 ,Valiant和 Kearns首次提出了 PAC學習模型中弱學習演演算法和強學習演演算法的等價性問題,即任意給定僅比隨機猜測略好的弱學習演演算法 ,是否可以將其提升為強學習演演算法 ? 如果二者等價 ,那麼只需找到一個比隨機猜測略好的弱學習演演算法就可以將其提升為強學習演演算法 ,而不必尋找很難獲得的強學習演演算法。1990年, Schapire最先構造出一種多項式級的演演算法 ,對該問題做了肯定的證明 ,這就是最初的 Boosting演演算法。一年後 ,Freund提出了一種效率更高的Boosting演演算法。但是,這兩種演演算法存在共同的實踐上的缺陷 ,那就是都要求事先知道弱學習演演算法學習正確的下限。1995年 , Freund和 schap ire改進了Boosting演演算法 ,提出了 AdaBoost (Adap tive Boosting)演演算法[ 5 ],該演演算法效率和 Freund於 1991年提出的 Boosting演演算法幾乎相同 ,但不需要任何關於弱學習器的先驗知識 ,因而更容易應用到實際問題當中。之後 , Freund和 schapire進一步提出了改變 Boosting投票權重的 AdaBoost . M1,AdaBoost . M2等演演算法 ,在機器學習領域受到了極大的關注。
Boosting方法是一種用來提高弱分類演演算法準確度的方法,這種方法通過構造一個預測函數系列,然後以一定的方式將他們組合成一個預測函數。他是一種框架演演算法,主要是通過對樣本集的操作獲得樣本子集,然後用弱分類演演算法在樣本子集上訓練生成一系列的基分類器。他可以用來提高其他弱分類演演算法的識別率,也就是將其他的弱分類演演算法作為基分類演演算法放於Boosting 框架中,通過Boosting框架對訓練樣本集的操作,得到不同的訓練樣本子集,用該樣本子集去訓練生成基分類器;每得到一個樣本集就用該基分類演演算法在該樣本集上產生一個基分類器,這樣在給定訓練輪數 n 后,就可產生 n 個基分類器,然後Boosting框架演演算法將這 n個基分類器進行加權融合,產生一個最後的結果分類器,在這 n個基分類器中,每個單個的分類器的識別率不一定很高,但他們聯合后的結果有很高的識別率,這樣便提高了該弱分類演演算法的識別率。在產生單個的基分類器時可用相同的分類演演算法,也可用不同的分類演演算法,這些演演算法一般是不穩定的弱分類演演算法,如神經網路(BP) ,決策樹(C4.5)等。
大多數提升演演算法包括由迭代使用弱學習分類器組成,並將其結果加入一個最終的成強學習分類器。加入的過程中,通常根據它們的分類準確率給予不同的權重。加和弱學習者之後,數據通常會被重新加權,來強化對之前分類錯誤數據點的分類。
一個經典的提升演演算法例子是AdaBoost。一些最近的例子包括LPBoost、TotalBoost、BrownBoost、MadaBoost及LogitBoost。許多提升方法可以在AnyBoost框架下解釋為在函數空間利用一個凸的誤差函數作梯度下降。
Boosting系列演演算法最經典的包括AdaBoost演演算法和GBDT演演算法。
AdaBoost,是英文"Adaptive Boosting"(自適應增強)的縮寫,由Yoav Freund和Robert Schapire在1995年提出。它的自適應在於:前一個基本分類器分錯的樣本會得到加強,加權后的全體樣本再次被用來訓練下一個基本分類器。同時,在每一輪中加入一個新的弱分類器,直到達到某個預定的足夠小的錯誤率或達到預先指定的最大迭代次數 。
具體說來,整個Adaboost 迭代演演算法就3步:
初始化訓練數據的權值分佈。如果有N個樣本,則每一個訓練樣本最開始時都被賦予相同的權值:1/N。
訓練弱分類器。具體訓練過程中,如果某個樣本點已經被準確地分類,那麼在構造下一個訓練集中,它的權值就被降低;相反,如果某個樣本點沒有被準確地分類,那麼它的權值就得到提高。然後,權值更新過的樣本集被用於訓練下一個分類器,整個訓練過程如此迭代地進行下去。
將各個訓練得到的弱分類器組合成強分類器。各個弱分類器的訓練過程結束后,加大分類誤差率小的弱分類器的權重,使其在最終的分類函數中起著較大的決定作用,而降低分類誤差率大的弱分類器的權重,使其在最終的分類函數中起著較小的決定作用。換言之,誤差率低的弱分類器在最終分類器中占的權重較大,否則較小。
GBDT也是集成學習Boosting家族的成員,但是卻和傳統的Adaboost有很大的不同。回顧下Adaboost,我們是利用前一輪迭代弱學習器的誤差率來更新訓練集的權重,這樣一輪輪的迭代下去。GBDT也是迭代,使用了前向分佈演演算法,但是弱學習器限定了只能使用CART回歸樹模型,同時迭代思路和Adaboost也有所不同。
在GBDT的迭代中,假設我們前一輪迭代得到的強學習器是ft−1(x)ft−1(x), 損失函數是L(y,ft−1(x))L(y,ft−1(x)), 我們本輪迭代的目標是找到一個CART回歸樹模型的弱學習器ht(x)ht(x),讓本輪的損失函數L(y,ft(x)=L(y,ft−1(x)+ht(x))L(y,ft(x)=L(y,ft−1(x)+ht(x))最小。也就是說,本輪迭代找到決策樹,要讓樣本的損失盡量變得更小。
GBDT的思想可以用一個通俗的例子解釋,假如有個人30歲,我們首先用20歲去擬合,發現損失有10歲,這時我們用6歲去擬合剩下的損失,發現差距還有4歲,第三輪我們用3歲擬合剩下的差距,差距就只有一歲了。如果我們的迭代輪數還沒有完,可以繼續迭代下面,每一輪迭代,擬合的歲數誤差都會減小。
由於Boosting演演算法在解決實際問題時有一個重大的缺陷,即他們都要求事先知道弱分類演演算法分類正確率的下限,這在實際問題中很難做到。後來 Freund 和 Schapire提出了 AdaBoost 演演算法,該演演算法的效率與 Freund 方法的效率幾乎一樣,卻可以非常容易地應用到實際問題中。AdaBoost 是Boosting 演演算法家族中代表演演算法,AdaBoost 主要是在整個訓練集上維護一個分佈權值向量 Dt( x) ,用賦予權重的訓練集通過弱分類演演算法產生分類假設 Ht ( x) ,即基分類器,然後計算他的錯誤率,用得到的錯誤率去更新分佈權值向量 Dt( x) ,對錯誤分類的樣本分配更大的權值,正確分類的樣本賦予更小的權值。每次更新後用相同的弱分類演演算法產生新的分類假設,這些分類假設的序列構成多分類器。對這些多分類器用加權的方法進行聯合,最後得到決策結果。這種方法不要求產生的單個分類器有高的識別率,即不要求尋找識別率很高的基分類演演算法,只要產生的基分類器的識別率大於 0.5 ,就可作為該多分類器序列中的一員。
尋找多個識別率不是很高的弱分類演演算法比尋找一個識別率很高的強分類演演算法要容易得多,AdaBoost 演演算法的任務就是完成將容易找到的識別率不高的弱分類演演算法提升為識別率很高的強分類演演算法,這也是 AdaBoost 演演算法的核心指導思想所在,如果演演算法完成了這個任務,那麼在分類時,只要找到一個比隨機猜測略好的弱分類演演算法,就可以將其提升為強分類演演算法,而不必直接去找通常情況下很難獲得的強分類演演算法。通過產生多分類器最後聯合的方法提升弱分類演演算法,讓他變為強的分類演演算法,也就是給定一個弱的學習演演算法和訓練集,在訓練集的不同子集上,多次調用弱學習演演算法,最終按加權方式聯合多次弱學習演演算法的預測結果得到最終學習結果。包含以下2 點:
樣本的權重
AdaBoost 通過對樣本集的操作來訓練產生不同的分類器,他是通過更新分佈權值向量來改變樣本權重的,也
就是提高分錯樣本的權重,重點對分錯樣本進行訓練。
(1) 沒有先驗知識的情況下,初始的分佈應為等概分佈,也就是訓練集如果有 n個樣本,每個樣本的分佈概率為1/ n。
(2)每次循環后提高錯誤樣本的分佈概率,分錯的樣本在訓練集中所佔權重增大,使得下一次循環的基分類器
能夠集中力量對這些錯誤樣本進行判斷。
弱分類器的權重
最後的強分類器是通過多個基分類器聯合得到的,因此在最後聯合時各個基分類器所起的作用對聯合結果有很大的影響,因為不同基分類器的識別率不同,他的作用就應該不同,這裡通過權值體現他的作用,因此識別率越高的基分類器權重越高,識別率越低的基分類器權重越低。權值計算如下:
基分類器的錯誤率:
e = ∑( ht ( x i) ≠yi) Di (1)
基分類器的權重:W t = F( e) ,由基分類器的錯誤率計算他的權重。
演演算法流程及偽碼描述
演演算法流程描述
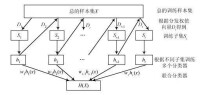
圖 1 演演算法流程
演演算法偽碼描述
輸入: S = { ( x1 , y1 ) , …( x i , y i) …, ( x n , y n) } , x i ∈X
yi ∈Y ;訓練輪數為 T; 初始化分發權值向量:
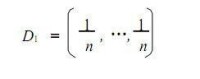
公式
for t = 1 , …, T :
(1) 使用分發權值向量 Dt訓練基分類器ht = R( x , y ,Dt) ; R為一弱的分類演演算法;
(2) 計算錯誤率:e = ∑( ht ( x i) ≠y i) Di (3)
(3) if e≥ 0.5 ,break ;
(4) 計算基分類器的權值 ht :wt ∈w;
(5) 更新權值:Dt ( i+1) = Dt ( i) ×F( e) (4)
其中 F( x)為更新函數,他以該次得到的基分類器的分類
錯誤率 e為自變數;
(6) 將多個基分類器進行聯合,輸出最後的分類器。
在上面的演演算法中:
①x i ∈X , yi ∈Y , x i 表示樣本屬性組成的向量, yi 表示該樣本的類別標籤;
②Dt 為樣本的分發權值向量:沒有先驗知識的情況下,初始的分佈應為等概率分
布,也就是訓練集如果有 n個樣本,每個樣本的分佈概率為1/ n;
每次循環后提高錯誤樣本的分佈概率,分錯的樣本在訓練集中所佔權重增大,使得下一次循環的弱學習演演算法能
夠集中對這些錯誤樣本進行判斷;Dt 總和應該為1 ;
③wt 為分類器的權值:準確率越高的分類器權重 w越大。
