共找到2條詞條名為損失函數的結果 展開
- 損失函數
- 成本函數
損失函數
損失函數
損失函數是徠指一種將一個事件(在一個樣本空間中的一個元素)映射到一個表達與其事件相關的經濟成本或機會成本的實數上的一種函數。損失函數(loss function)或代價函數(cost function)是將隨機事件或其有關隨機變數的取值映射為非負實數以表示該隨機事件的“風險”或“損失”的函數。在應用中,損失函數通常作為學習準則與優化問題相聯繫,即通過最小化損失函數求解和評估模型。例如在統計學和機器學習中被用於模型的參數估計(parametric estimation) ,在宏觀經濟學中被用於風險管理(risk mangement)和決策,在控制理論中被應用於最優控制理論(optimal control theory)。
在樣本空間內有可測狀態和隨機變數根據法則所做的決策,此時若在乘積空間上有函數滿足:,即對任意的,是非負可測函數,則被稱為損失函數,表示狀態下採取決策所對應的損失或風險。
機器學習中,給定獨立統一分佈(independent and identically distributed,iid)的學習樣本,和模型,損失函數是模型輸出和觀測結果間概率分佈差異的量化:
式中表示模型參數,上式右側具體的量化方法視問題和模型而定,但要求滿足損失函數的一般定義,即樣本空間的非負可測函數。
回歸問題
回歸問題所對應的損失函數為L2損失函數和L1損失函數,二者度量了模型估計值與觀測值之間的差異:
式中為真實值的權重,為真實值,為模型的輸出。各類回歸模型,例如線性回歸、廣義線性模型(Generalized Linear Model, GLM)和人工神經網路(Artificial Neural Network, ANN)通過最小化L2或L1損失對其參數進行估計。L2損失和L1損失的不同在於,L2損失通過平方計算放大了估計值和真實值的距離,因此對偏離觀測值的輸出給予很大的懲罰。此外,L2損失是平滑函數,在求解其優化問題時有利於誤差梯度的計算;L1損失對估計值和真實值之差取絕對值,對偏離真實值的輸出不敏感,因此在觀測中存在異常值時有利於保持模型穩定。
分類問題
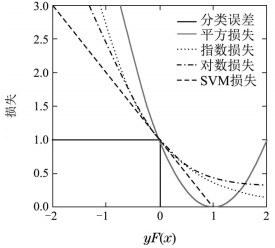
分類問題所對應的損失函數為0-1損失,其是分類準確度的度量,對分類正確的估計值取0,反之取1:
0-1損失函數是一個不連續的分段函數,不利於求解其最小化問題,因此在應用可構造其代理損失(surrogate loss)。代理損失是與原損失函數具有相合性(consistency)的損失函數,最小化代理損失所得的模型參數也是最小化原損失函數的解。當一個函數是連續凸函數,並在任意取值下是0-1損失函數的上界時,該函數可作為0-1損失函數的代理函數。
這裡給出二元分類(binary classification)中0-1損失函數的代理損失:
| 二元分類中常見的代理損失 | |
| 名稱 | 表達式 |
|---|---|
| 鉸鏈損失函數(hinge loss function) | |
| 交叉熵損失函數(cross-entropy loss function) | |
| 指數損失函數(exponential loss function) |
鉸鏈損失(實線)、交叉熵損失(點)、指數損失(虛線)
鉸鏈損失函數是一個分段連續函數,其在分類器分類完全正確時取0。使用鉸鏈損失對應的分類器是支持向量機(Support Vector Machine, SVM),鉸鏈損失的性質決定了SVM具有稀疏性,即分類正確但概率不足1和分類錯誤的樣本被識別為支持向量(support vector)被用於劃分決策邊界,其餘分類完全正確的樣本沒有參與模型求解。
交叉熵損失函數是一個平滑函數,其本質是信息理論(information theory)中的交叉熵(cross entropy)在分類問題中的應用。由交叉熵的定義可知,最小化交叉熵等價於最小化觀測值和估計值的相對熵(relative entropy),即兩者概率分佈的Kullback-Leibler散度:,因此其是一個提供無偏估計的代理損失。交叉熵損失函數是表中使用最廣泛的代理損失,對應的分類器例子包括logistic回歸、人工神經網路和概率輸出的支持向量機。
指數損失函數是表中對錯誤分類施加最大懲罰的損失函數,因此其優勢是誤差梯度大,對應的極小值問題在使用梯度演演算法時求解速度快。使用指數損失的分類器通常為自適應提升演演算法(Adaptive Boosting, AdaBoost),AdaBoot利用指數損失易於計算的特點,構建多個可快速求解的“弱”分類器成員並按成員表現進行賦權和迭代,組合得到一個“強”分類器並輸出結果。
損失函數
現在舉個例子:某個工廠人員的產出,以每小時多少元來計算,而損失函數所顯示的,是產出以室內通風條件而改變的情形。廠內工作的每個人,都有自己的損失函數。為了簡化說明,假設每個人的損失函數均為一條拋物線,其底部一點代表產出值最大時的通風條件,把所有人員的損失函數進行疊加,公司整體的損失函數也必然是一條拋物線。如果通風條件偏離這個最佳水準,就會有額外損失發生。
該拋物線與橫軸相切時,切點的左右各有一小段與橫軸幾近重合。也就是說,有最適點偏離一小短距離,損失小到可以忽略不計。因此,當室內通風條件稍稍偏離均衡點,發生的損失可以忽略不計。
但是遠離均衡點時,總是有人必須支付這損失。如果我們能夠導出有具體數字的損失函數,我們就可以計算出最有均衡點,在均衡點中最適合的通風條件如何,以及達到要求的費用支出是多少。
損失函數並非一定是對稱的。有時候其中一邊很陡峭,有時候則兩邊都很陡峭。舉例而言,為了使鋼片較容易焊接,需要加入鈳。但鈳的加入量如果低於必須量,純粹是浪費,對焊接一點益處都沒有。然而鈳用量如高於十萬分之一,也是一種浪費,所增加的利益相當有限。
戴明博士曾在《企業研究的樣本設計》(Sample Design in Business Research)一書內,列示了一個實際的損失函數。它顯示我們只需要盡量靠近樣本的最有組合就行了,只要非常接近就可以了。
以趕火車作為符合規格的例子。假設我們的時間價值為每分鐘n元,下圖左邊的斜線是損失線的斜率;早一分鐘到達月台,將讓我們損失n元,早兩分鐘到達損失2n元。另一方面,如果沒有趕上火車,我們的損失是M元。遲到半分鐘或遲到5分鐘損失一樣,損失函數直接由零跳到M。
每天趕火車是一個重複進行的事件,我們試著畫出到達時間的分配曲線,其最右端(三個標準差界限)恰好為火車離站時間。換句話說,我們使用變異知識之後,平均每日損失率變成下圖中損失函數下的陰影部分。
當然問題也可複雜化,例如火車每天離站的時間也有變化,所以也可以畫出一個分配圖。火車到站時間三個標準差的界限可能是8秒。把問題這樣複雜化,對於我們了解和應用損失函數並沒有特別大的幫助,因此我們就說到這裡。另一個例子,是參加星期日早上11點15分的禮拜時所碰到的停車問題。教堂的停車場最大負荷是停放50輛車子,但這些車位在10點50分左右仍然客滿,因為作完上一場禮拜的車主仍在喝咖啡。等他們一離開,這些空位馬上就會被排成長龍等待的車隊填滿。如果你想佔到一個車位,不得不早早去排隊。那些晚到的人在這裡找不到車位,只能到街上去找,但實際上往往無功而返。所以,上策還是提早一點去等,承受等待的損失而能佔到位置。
這項理論也可以應用到任何計劃的截止時間上。某人要求必須在截止日期前完成工作,萬一未能趕上這個時間,勢將使計劃延誤或出錯。為了能準時完成,可以擬定工作內容與步驟的綱要。把個步驟的截止日期設定一段期間要比設定為固定的從容,而且有時間作最後的修訂,可能把計劃做得更好。
我們在這裡再次提及一些老生常談,就是千萬不要以符合規格為自滿。那麼我們的產出水準在最低損失的位置嗎?假設損失函數為
L(徠x)=ax (拋物線)
則x為0時,損失為最小。至於生產的損失函數是:
∫-∞L(x)P(x)=f(u,б)
顯然u為零時損失最小,因此我們努力的目標,應該把生產移向目標值,即u為零。
以上所敘述的並不是什麼新理論。此外,多年前貝提(John Betti)在福特汽車公司所說的一段話也值得引述:“我們美國人關心的是符合規格;相反地,日本人則齊心一致,儘力減少與目標值的變異。”
由此可知,某項產出的散布(dispersion)情況,並不能作為成就的指標。事實上,中心線的位置才是最重要的,我們當然應該努力使任何生產的散布儘可能縮小,但是那只是第一步。下一個重要的步驟是使中心位置在目標值上。
這些簡單的說明,可促使我們了解,如Cpk這種測度散布情況的測度毫無價值,因為它們對評估損失來說毫無意義可言。此外,只要放寬規格,就可以使該值低至任何數值。無論是符合規格、零缺陷或其他秘方,都沒有找到問題的關鍵所在。