成本函數
成本函數
成本函數(cost function)指在技術水平和要素價格不變的條件下,成本與產出之間的相互關係。成本理論主要分析成本函數。成本函數和成本方程不同,成本函數說的是成本和產量之間的關係,成本方程說的是成本等於投入要素價格的總和,如果投入的是勞動L和資本K,其價格為PL和PK,則成本方程是C=L·PL+K·PK,成本方程是一個恆等式,而成本函數則是一個變數為產量的函數式。
在統計學中,成本函數(cost function)通常被稱為損失函數(loss function)。
用表格表示長短期成本函數的基本情況:
| 長期成本函數 | 短期成本函數 | |
| 模型 | MINC=(W1X1+W2X2) s.t.f(X1,X2)=y | MINC=(W1X1+W2X2) s.t.f(X1,X2)=yX2=X2 |
| 外生變數 | W1,W2,Y | W1,W2,Y,X |
| 內生變數 | X1*,X2*,c* | X1*,c* |
| 條件要素需求函數 | X1=X1(W1,W2,Y) X2=X2(W1,W2,Y) | X1=X1(W1,W2,Y,X) X2=X2(W1,W2,Y,X) |
| 成本函數 | C(W1,W2,Y) | C(W1,W2,Y,X) |
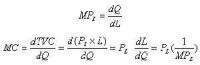
成本函數
從模型的描述和比較W1,W2,很容易得到一些關於長期成本函數和短期成本函數的關係。
性質1:給定要素價格,對任意的產量y,和任意的固定要素量X2,一定有C(W1,W2,Y))≤C(W1,W2,Y,X)。
證明:因為短期成本函數模型相對與長期成本函數的模型,所有條件都一樣,只是增加了一條約束條件。所以短期成本函數模型中的可行域小於長期成本函數模型的可行域,從而前者的最小目標函數值不可能比後者的最小目標函數值值更小。而模型最小目標函數值正是成本函數值。
說明:這條性質說明,長期成本曲線在任意一條短期成本曲線的下方。
成本函數
證明:事實上,取*x2=x2=x2(w1,w2,y),則從預算約束的成立,可以推知,一定有x(w1,w2,y,x)=x(w1,w2,y),從而:C(w1,w2,y)=w1x1(w1,w2,y)+w2x2*=wx1(w,w,y,x*)+w2x2*=C(w1,w2,y,x*)。
說明:這條性質說的是,長期成本上的任意一點,都有一條短期成本線可以達到它。
性質3:給定要素價格W1,W2,對任意的產量y,由性質2知道存在某個固定要素量X2,使得C(w1,w2,y)=C(w1,w2,y,x)。那麼對於任意的y′≠y,一定有1:C(w1,w2,y′)
證明:因為在y′下,要素x1=x1(w1,w2y′),x2=x2(w1,w2,y′)是最優選擇,所以對任意能生產出y′的其他要素組合x1′,x2′,一定有:w1x1(w1,w2,y′)+w2x2(w1,w2,y′)

成本函數
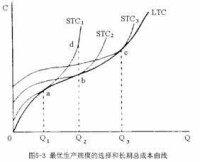
性質1,2描述的一般性曲線關係,就叫做“包絡”關係。說白了,就是包絡線在下面,包住了所有曲線,並且包絡線的每一點,要能被曲線族中的某一條曲線取到。上述是成本曲線的關係,平均成本曲線就是在所有等式、不等式兩邊同除以y,所有性質還是成立的。於是,長期平均成本一樣是短期平均成本的包絡線。
短期成本函數反映了在技術、規模、要素價格給定條件下,最低成本隨著產量變動而變動的一般規律。技術水平是通過生產函數來刻劃的。因此,成本函數和生產函數之間存在著非常密切的關係。若給定生產函數和要素價格,就可以推導出成本函數。
成本函數
長期總成本曲線的陡峭程度完全取決於生產函數和生產要素的價格。此曲線表現出這樣幾項特點:其一,成本和產量有直接關係,從上圖中可以看出曲線有正科率,它表明產量增加,總成本就會增加,說明資源是有限的。其二,LRTC曲線先以一逐漸遞減的比率,然後再以一個逐漸遞增的比率上升,從上可以看出X產量的增量是相對的,而C成本的增量先是遞減,然後是遞增,即X1X2=X2X3時,但C1C2>C2C3,相反,當X4X5=X5X6jf,C4C5>C5C6。
從短期來看,企業耗費的成本有一總值是固定的,如廠房設備折舊費等,有一部分則是變化的,如原材料、人工費等。所以,產品的短期總成本總是等於固定總成本與總變動成本之和,短期總成本曲線就是短期總成本函數的圖象表示。
下面是一個具體的例子。

成本函數
約束函數:
要素價格:
則要素邊際產量:
最低成本的要素投入組合的必要條件:
由此得到要素最佳投入比例:
分別將(3)、(4)代人生產函數(1)得:
將(5)代人約束函數(2)得:
就是(6)
(6)就是得到的成本函數。該成本函數的邊際成本和平均成本都是常數,不具有典型形態。
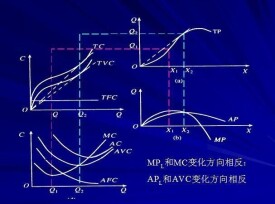
經濟分析中的成本曲線和生產曲線具有非常工整的對應關係:
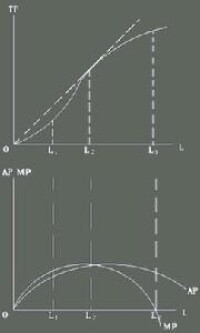
1、總產量曲線和總成本曲線:
隨著變動要素投入量的增加,總產量先遞增地增加,然後遞減地增加。與此對應,隨著產量的增加,總成本先遞減地增加,然後遞增地增加。
2、邊際產量曲線與邊際成本曲線:

成本函數
3、平均產量曲線與平均變動成本曲線:
隨著勞動投入的增加,平均產量先提高,後下降。與此對應,隨著產量的增加,平均變動成本先下降,後上升。使平均產量最大的變動要素投入量,對應於平均變動成本最低的產量