正規族

如果從全純函數族 F的每一個函數序列 ƒn(z)(n＝1,2,…)中，都可以選出一個子序列 ƒ(z)(k=1,2,…)在D 的內部一致收斂到一個全純函數或一致收斂到常量∞，則區域D內的全純函數族F稱為在D內為正規的。

因此，一個全純函數族F在一個區域D內為正規的一個充分條件是F中的函數在D內均不取同一個圓C外之值，另一個充分條件是不取 C內之值。凡是這樣的充分條件都稱為正規性定則。經過進一步的研究，蒙泰爾證明了：F中的函數在D內均不取兩個固定的有窮值α及b，是一個正規性定則。這個定則可使複變函數論中過去看來是鬆散的幾個定理呈現緊密的聯繫，如從這個定則很容易推出皮卡第一定理：一個非常數的整函數ƒ（z）取每一個有窮值，最多除去一個例外值。證明方法是引進函數序列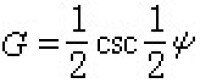，如果以上皮卡定理不成立，則根據蒙泰爾的正規性定則，這個函數序列構成在圓｜z｜<2內的一個正規族，而導出矛盾。用類似的方法，也可以從蒙泰爾的正規性定則推出皮卡第二定理：如果一個函數ƒ(z)在一區域0<｜z｜<ρ為全純並以z＝0為本性奇點，則在此區域內函數ƒ(z)取每一有窮值無窮次，最多除去一個例外值。根據蒙泰爾的正規性定則還可以證明下列朔特基定理：如果一函數ƒ(z)在一圓｜z｜柯西不等式，又可推出蘭道定理：如果一函數ƒ(z)滿足朔特基定理中條件並且ƒ′(0)≠0，則R不超過一個只依賴於ƒ(0)及ƒ′(0)的上限。

蒙泰爾引進正規族的概念之後，又進一步引進了擬正規族的概念。全純函數擬正規族的定義和全純函數正規族的定義的差別是：不要求子序列 ƒ(z)(k=1,2,…)在D的內部一致收斂，而只要求除去D內有窮個點（或無窮個點，但在D內沒有凝聚點）后，在所余的區域內部一致收斂，然後他將G.維塔列的一個定理推廣為：如果在一個區域D 的一個全純函數序列屬於一個正規族或擬正規族，並且在D內無窮個點收斂到有窮極限，而這無窮個點在D內最少有一個凝聚點，則此全純函數序列在D的內部一致收斂。

經過C.卡拉西奧多里、E.G.H.蘭道、蒙泰爾及A.奧斯特羅夫斯基的工作，亞純函數正規族的理論也建立起來。如果一致收斂性是用球面距離來定義，那麼亞純函數正規族的定義如下：如果從亞純函數族F的每一個函數序列ƒn(z)(n=1,2,…)中，都可以選出一個子序列ƒ(z)(k=1,2,…)在一個區域D的內部一致收斂，則D內的亞純函數族F稱為在D內為正規的。關於亞純函數族蒙泰爾的正規性定則是：F中的函數在D內均不取三固定的值α，b及с（有窮或無窮）。類似地也可以給出亞純函數擬正規族的定義。

全純函數正規族及亞純函數正規族的理論已經發展到完善的地步。這個理論中的一個重要研究問題是尋求新的正規性定則。關於這個問題已有許多工作，在這方面,A.布洛赫的下列猜測很有指導意義：如果p是一個性質，非常數的整函數不具有性質p,那麼在一個區域內具有性質p 的全純函數族是正規的。這個猜測在一些例子中都是對的。例如，與關於整函數的劉維爾定理相應的是以上蒙泰爾的關於一致有界的全純函數族的定理；與關於整函數的皮卡定理相應的是以上蒙泰爾的關於有兩個例外值的全純函數族的定則。此外，布洛赫還根據他的下列定理：如果函數ƒ(z)於｜z｜<1為全純,ƒ(0)=0並且ƒ′(0)＝1，則存在一個半徑大於一絕對常數的圓，在其中函數ƒ(z)的反函數有一分支為全純；推出了一個新的正規性定則：在一個區域D 的全純函數族F,如果F 中的函數的反函數的全純圓域的半徑小於一個固定的常數，那麼F在D為正規。

參考書目

P.Montel,Léons sur les familles NorMales de Fonctions Analytiques et Leurs Applications, Gauthier-Villars,Paris, 1927.

G.Valiron,familles NorMales et Quasi-norMales de Fonctions Méromorphes,Mémorial des Sc. Math., fasc.38, Gauthier-Villars, Paris, 1929.