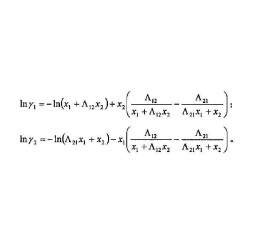1964年,Wilson從Fory-Huggins方程發,提出了用於描述非電解質溶液的過量吉布斯自由能(Gibbs)的方程,即威爾遜(Wilson)方程。該方程對有機化學溶液的熱力學性質的預測取得了成功,利用Wilson方程僅需二元系的參數便可描述多元系的熱力學性質。
1964年Wilson 設想分子之間的相互作用主要取決於可用
體積分數表示的“局部濃度”,提出了著名的Wilson方程。這些濃度被定義為隨機項,即能量的Boltzmann 分佈。對於包含1和2兩種類型分子的混合物,在類型1和2的分子附近出現同類型其它分子的概率記為和,出現另一類型分子的概率分別記為和,則兩種概率的比值為
用這些概率表示的體積分數為
上式中,表示
組元i的摩爾體積,,並定義Wilson參數為:
假設Gibbs自由能依賴於,則理想值 依賴於。所以過量Gibbs自由能的表達式為

威爾遜方程
威爾遜方程對有機化學溶液的熱力學性質的預測取得了成功。Wilson曾將該方程用於
四氯化碳-乙腈和四氯化碳.
硝基甲烷二元系,該兩個二元系的過量Gibbs自由能的計算值與實驗值非常接近。如下圖:
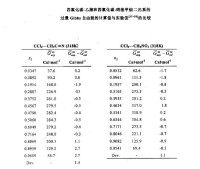
威爾遜方程
1970年Tabby等 將Wilson方程用於Fe-Cu和Fe-Ni二元液態合金體系組元活度的擬合,並將擬合結果與實驗數據進行了比較。雖然較Darken方程 的擬合結果稍差一些,但由於Wilson方程僅需兩個參數,其擬合效果還是令人滿意的。1991年Wilson方程被首次應用於三元液態合金的熱力學性質預測,對和兩個三元系中組元Cd的活度進行了計算,取得了成功。隨後該方程在四元、
五元液態合金和液態爐渣及熔鹽的熱力學性質計算方面也取得了進展。我們曾將Wilson方程用於對二元鋁基液態合金組元的熱力學性質的計算,將二元鋁基合金體系分為強偏差體系、弱偏差體系和混合偏差體系進行了系統的比較研究,結果表明,其組元的活度或
活度係數的擬合偏差均接近或小於實驗偏差。後來又將其應用於三元系中組元活度的預測50,也取得了令人滿意的結果。