諾模圖
1884年法國奧卡涅提出的理論
諾模圖的種類很多,有共線圖和共點圖(也稱網路圖)等,通常說的諾模圖是指共線圖。共線圖的理論是由法國的奧卡涅於1884年首先提出的。
根據一定的幾何條件(如三點共線),把一個數學方程的幾個變數之間的函數關係,畫成相應的用具有刻度的直線或曲線表示的計算圖表。是工程技術上常用的一種計算圖表。諾模圖使用方便,求解迅速,可以避免大量的重複計算,因此在 機械設計中得到廣泛的應用。
諾模圖的種類很多,有共線圖和共點圖(也稱網路圖)等。通常說的諾模圖是指共線圖。共線圖的理論是由法國的奧卡涅於1884年首先提出的。
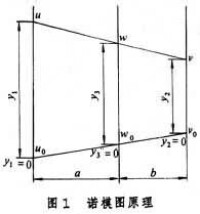
共線圖是用 3個圖尺表示一個包含3個變數的方程。在這些圖尺上,凡是標值滿足該方程的3個刻度點都必須位於同一直線上(圖1、圖2)。其中最常用的是由 3條平行直線圖尺組成的共線圖,其典型方程為。使用共線圖時,如已知兩個變數,則過該兩變數的圖尺上相應的變數點作一直線,該直線與第三圖尺的交點就是所求第三變數的值。
諾模圖的基本概念是圖尺、圖尺係數和圖尺方程。
諾模圖
② 圖尺係數:表示函數值單位的長度,記作m。以L表示直線圖尺的長度,變數u的標值範圍從到,相應的函數值為和 ,則圖尺係數為。
③ 圖尺方程:圖尺上刻度所依據的方程式。若所畫的函數為f(u),刻度的原點為,從原點到任一刻度u所量得的距離為y,則圖尺方程為。因此圖 1中的三平行尺共線圖中三條圖尺的方程分別為
u圖尺
v圖尺
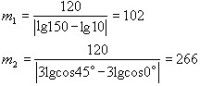
諾模圖
圖尺距離
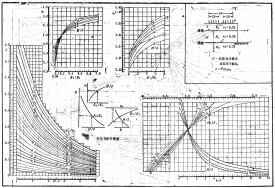
若常用齒數範圍 ,常用螺旋角範圍,得出圓化值;取圖尺長度毫米,則圖尺係數分別為 為刻度方便,取,得三條圖尺的方程為
Z 圖尺
β圖尺
Z′圖尺

諾模圖
若選取,則。畫出共線圖(圖2)。
使用時,若已知,則通過這兩點作一直線,在與Z′圖尺的交點處讀得。