檢驗統計量
用於假設檢驗計算的統計量
檢驗統計量是用於假設檢驗計算的統計量。在零假設情況下,這項統計量服從一個給定的概率分佈,而這在另一種假設下則不然。從而若檢驗統計量的值落在上述分佈的臨界值之外,則可認為前述零假設未必正確。統計學中,用於檢驗假設量是否正確的量。常用的檢驗統計量有t統計量,Z統計量等。
根據樣本觀測結果計算得到的,並據以對原假設和備擇假設做出決策的某個樣本統計量,稱為檢驗統計量。
檢驗統計量是用於假設檢驗計算的統計量,實際上是對總體參數的點估計量,但點估計量不能直接作為檢驗的統計量,只有將其標準化后,才能用於度量它與原假設的參數值之間的差異程度。而對點估計量的標準化依據原則是:
(1)原假設為真;
(2)點估計量的抽樣分佈。
通常將標準化統計量簡稱為檢驗統計量,標準化的統計量可表示為
能夠拒絕原假設的檢驗統計量的所有可能取值的集合,稱為拒絕域;不能夠拒絕原假設的檢驗統計量的所有可能取值的集合稱為接受域;根據給定的顯著性水平確定的拒絕域的邊界值,稱為臨界值。
拒絕域就是由顯著性水平所圍成的區域。如果利用樣本觀測結果計算出來的檢驗統計量的具體數值落在了拒絕域內,就拒絕原假設,否則就不能拒絕原假設。
拒絕域的大小與人們事先選定的顯著性水平有一定關係。在確定了顯著性水平之後,就可以根據α值的大小確定出拒絕域的具體邊界值。
在給定顯著性水平后,查統計表就可以得到具體的臨界值(也可以直接由Excel中的函數命令計算得到)。將檢驗統計量的值與臨界值進行比較,就可做出拒絕或不拒絕原假設的決策。
當樣本量固定時,拒絕域的面積隨著α的減小而減小。α值越小,為拒絕原假設所需要的檢驗統計量的臨界值與原假設的參數值就越遠。拒絕域的位置取決於檢驗是單側檢驗還是雙側檢驗。雙側檢驗的拒絕域在抽樣分佈的兩側。而單側檢驗中,如果備擇假設具有符號“<”,拒絕域位於抽樣分佈的左側,稱為左側檢驗;如果備擇假設具有符號“>”,拒絕域位於抽樣分佈的右側,稱為右側檢驗。
在給定顯著性水平α下,拒絕域和臨界值如圖2、3、4所示。
統計決策所依據的規則如下:
(1)給定顯著性水平,查表得出相應的臨界值或,或;
(2)將檢驗統計量的值與水平的臨界值進行比較;
(3)做出決策:
雙側檢驗∣統計量的值∣>臨界值,拒絕;
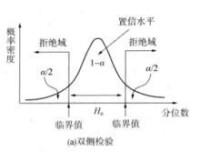
圖2
左側檢驗統計量的值<-臨界值,拒絕;
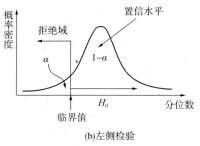
圖3
右側檢驗統計量的值>臨界值,拒絕。
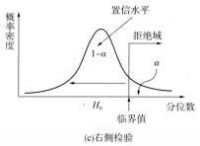
圖4
