混疊
混疊
混疊(英語:Aliasing),在信號頻譜上可稱作疊頻;在影像上可稱作疊影,主要來自於對連續時間信號作取樣以數字化時,取樣頻率低於兩倍奈奎斯特頻率。
在統計、信號處理和相關領域中,混疊是指取樣信號被還原成連續信號時產生彼此交疊而失真的現象。當混疊發生時,原始信號無法從取樣信號還原。而混疊可能發生在時域上,稱做時間混疊,或是發生在頻域上,被稱作空間混疊。
在視覺影像的模擬數字轉換或音樂信號領域,混疊都是相當重要的議題。因為在做模擬-數字轉換時若取樣頻率選取不當將造成高頻信號和低頻信號混疊在一起,因此無法完美地重建出原始的信號。為了避免此情形發生,取樣前必須先做濾波的操作。
(1)從時域信號重構看混疊
混疊
混疊
混疊
混疊
混疊
如下圖,圖中的信號是 的一部分,它的頻域只在 處有一條譜線。當用 進行採樣時,得到一條直流的曲線。當用 採樣的時候,得到一個三角波信號。當用 對它進行採樣的時候,也得到一個更低頻的三角波信號。採樣信號不僅不能重構原信號,出現混疊頻率,即採樣信號不能保持原信號的頻譜特性。
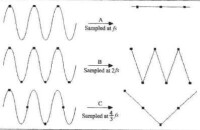
混疊
混疊
混疊
連續信號經過離散採樣后,得到的離散信號的傅氏譜為原信號傅氏譜SF倍的周期延拓,如果原信號中包含的最高頻率成分,則在離散信號譜中相應周期的譜會出現重疊。反之,如果,即採樣頻率大於分析信號中最高頻譜成分的2倍,則採樣后離散信號頻譜中不會出現頻率混疊。
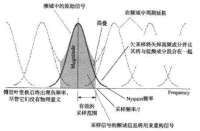
混疊
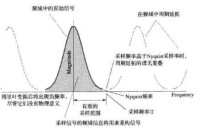
混疊
採樣定理的一個重要指導意義是給出了消除混疊的最低條件,混疊本身是採樣的必然效應,只不過如果混疊到原信號帶寬範圍內的頻率成分為零的話,信號不會被破壞,也就能“完全重構”了。消除頻率混疊的途徑有兩種:
混疊
混疊
(1)提高採樣頻率fs,即縮小採樣時間間隔。然而實際的信號處理系統不可能達到很大的採樣頻率。另外,許多信號本身可能含有 範圍內的頻率,不可能將採樣頻率提高到。所以,通過提高採樣頻率避免混疊的方法是有限制的。
(2)採用抗混濾波器。在採樣頻率fs一定的前提下,通過低通濾波器濾掉高於fs/2的頻率成分,通過低通濾波的信號則可避免出現頻率混疊。
在理想濾波的情形下,濾掉高於Nyquist頻率的信號成分即可不產生混疊。然而,實際的濾波器都不具有理想濾波器的特性,如下圖所示。所以,實際處理過程中一般應滿足下面的關係:
混疊

混疊
混疊
混疊
混疊
混疊
根據混疊機理,可以得出分析信號的混疊頻率計算公式,設實際信號的頻率為,採樣頻率為,並且,經採樣分析得到的混疊后頻率為,則有如下公式:
混疊
混疊
混疊
式中, ,其中 為取整操作,僅保留小數點的整數部分。
混疊
考慮一個有八個輻條車輪以3轉/秒(或180rpm)的轉速旋轉。在這種情況下,車輪會在每幀內移動一個輻條,因為:
混疊
考慮如果車輪以一個低於這個數值的速率轉動,比如2.5轉/秒。現在車輪將移動83%個輻條間距每幀。所以,比較兩個相鄰的幀,我們會看到下面的現象:
人的大腦在看這些電影幀的時候會存在兩個解釋。一個解釋是輪子已經移動了83%沿順時針方向輪輻間隔。另一種解釋就是它已經沿著逆時針方向移動了17%的輻條間隔。事實證明大腦喜歡後者的解釋,所以你感覺到的結果是車輪以比實際速度慢的速度向後(逆時針)移動移動。
混疊
混疊
混疊
混疊
所定的取樣頻率若取樣的頻率太低,就會產生取樣的結果和原來的樣本不同的狀況。若一樣本的頻譜是帶限頻譜,也就是在某一頻率 之外都為0的頻譜,那麼取樣頻率 就必須要大於兩倍的,才不至於使頻譜產生交疊,也因此產生失真。
混疊
