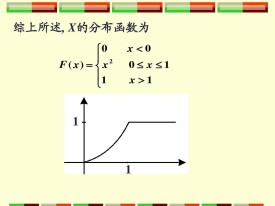
分佈函數
專業術語
分佈函數，專業術語，拼音為fēn bù hán shù，是數學概念上的一種函數，分佈函數主要反映數值的分佈，被廣泛應用於數學、經濟學、物理學、統計學等學科之中。
在數學意義上，我們將分佈函數的定義表述為：設X是一個隨機變數，x是任意實數，函數F(x)=PX≤x稱為X的分佈函數。有時也記為X~F(x)。
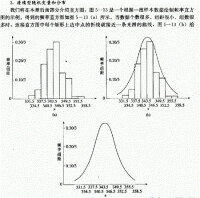
分佈函數
F(x)=P{X≤x}
稱為X的分佈函數。
對於任意實數x1,x2(x1＜x2),有
P{x1＜X≤x2}=P{X≤x2}-P{X≤x1}=F(x2)-F(x1),
因此，若已知X的分佈函數，就可以知道X落在任一區間(x1,x2]上的概率，在這個意義上說，分佈函數完整地描述了隨機變數的統計規律性。
分佈函數是一個普遍的函數，正是通過它，我們將能用數學分析的方法來研究隨機變數。
如果將X看成是數軸上的隨機點的坐標，那麼，分佈函數F(x)在x處的函數值就表示X落在區間(-∞,x]上的概率。
分佈函數P{x1＜X≤x2}=P{X≤x2}-P{X≤x1}=F(x2)-F(x1)≥0
證明：即對任意的X1>X2時，有F(X1)≤F(X1)，
這是因為P{x1＜X≤x2}=P{X≤x2}-P{X≤x1}=F(x2)-F(x1)≥0。
從而證明對任意的X1>X2時，有F(X1)≤F(X1)。
F(x)=F(x+0)。
F（-∞）=0，F（+∞）=1。
定理
1.分佈函數是對樣本空間的數學描述，為解析方法提供了可能。
2.不同性質的樣本空間對應不同的分佈函數。
3.目前常用分佈函數種類可滿足大多數需要。
求出該變數的分佈函數，需要了解以下信息：
1.你的數據所反應的事件的性質，從而粗略判斷可能的分佈函數形式。
2.根據所選定分佈函數形式，利用自己的數據求出相應參數(期望，方差等等)。
3.用所得的函數來檢驗你的數據，給出模擬曲線與解析曲線的偏差。
4.如果複合你需要的精度，就OK。
5.重複上述步驟。
基本信息
- 中文名
- 分佈函數
- 別名
- 累積分佈函數
- 外文名
- Cumulative Distribution Function
- 定義
- 描述隨機變數的概率分佈
- 功能
- 顯示隨機變數的分佈
- 適用領域
- 數學、金融、IT
- 領域
- 數學
- 記作
- Fx(x)