在數學中動態系統的概念里,二維流形或平面中的極限環是相平面中的一段閉合的軌跡。當時間趨於正無窮或負無窮(0)時,有至少一段其他的軌跡與其旋轉相交。極限環在非線性系統中經常能看到。在時間t趨於正無窮時附近所有的軌跡都逐漸靠近極限環的時候,這種極限環被稱為穩定的極限環。如果所有附近軌跡在t趨於負無窮時逐漸靠近極限環,這個極限環是不穩定的極限環。所有的極限環只有穩定和不穩定兩類。
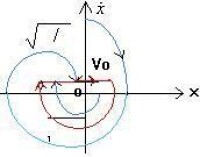
極限環
相平面內的封閉相軌跡與實際系統的周期運動相對應。保守系統在穩定平衡位置附近的等幅自由振動對應於相平面內圍繞中心奇點的封閉相軌跡族。在密集的封閉相軌跡族中,實際相軌跡的振幅由初始運動狀態確定。自激振動是一種特殊的周期運動,它的振幅和頻率由系統的物理參數惟一確定,與初始運動狀態無關。因此自激振動在相平面內的相軌跡是孤立的封閉曲線,稱作相平面的極限環。極限環可以是穩定的也可以不穩定。當相點由於擾動偏離極限環后,即沿新的相軌跡運動,若擾動后的相軌跡仍漸近地貼近極限環,則稱極限環是穩定的。反之,若擾動后的相軌跡遠離極限環,則極限環不穩定。只有穩定的極限環才是物理上可實現的自激振動。
參考資料:
1.
《振動力學》,劉延柱 陳文良 陳立群 編著,高等教育出版社,2008年4月第7次印刷
