墨卡托投影

墨卡托投影，是正軸等角圓柱投影，又稱等角圓柱投影，圓柱投影的一種，由荷蘭地圖學家墨卡托（G. Mercator）於1569年創擬。為地圖投影方法中影響最大的。

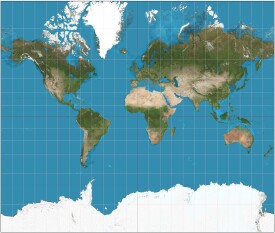
設想一個與地軸方向一致的圓柱切於或割於地球，按等角條件將經緯網投影到圓柱面上，將圓柱面展為平面后，得平面經緯線網。投影后經線是一組豎直的等距離平行直線，緯線是垂直於經線的一組平行直線。各相鄰緯線間隔由赤道向兩極增大。一點上任何方向的長度比均相等，即沒有角度變形，而面積變形顯著，隨遠離基準緯線而增大。該投影具有等角航線被表示成直線的特性，故廣泛用於編製航海圖和航空圖等。

墨卡托投影，是一種"等角正切圓柱投影”，由荷蘭地圖學家墨卡托（Gerhardus Mercator 1512－1594）在1569年擬定。

假設地球被圍在一中空的圓柱里，其基準緯線與圓柱相切（赤道）接觸，然後再假想地球中心有一盞燈，把球面上的圖形投影到圓柱體上，再把圓柱體展開，這就是一幅選定基準緯線上的“墨卡托投影”繪製出的地圖。墨卡托投影沒有角度變形，由每一點向各方向的長度比相等，它的經緯線都是平行直線，且相交成直角，經線間隔相等，緯線間隔從基準緯線處向兩極逐漸增大。墨卡托投影的地圖上長度和面積變形明顯，但基準緯線處無變形，從基準緯線處向兩極變形逐漸增大，但因為它具有各個方向均等擴大的特性，保持了方向和相互位置關係的正確。在地圖上保持方向和角度的正確是墨卡托投影的優點，墨卡托投影地圖常用作航海圖和航空圖，如果循著墨卡托投影圖上兩點間的直線航行，方向不變可以一直到達目的地，因此它對船艦在航行中定位、確定航向都具有有利條件，給航海者帶來很大方便。中華人民共和國國家標準“海底地形圖編繪規範”（GB/T 17834-1999）中5.1.3.1款規定 1：25萬及更小比例尺圖採用墨卡托投影，基本比例尺圖（即1：5萬，1：25萬，1：100萬）採用統一基準緯線30°，非基本比例尺圖以製圖區域中緯為基準緯線。基準緯線取至整度或整分。

基哈德斯·墨卡托於1512年出生在佛蘭德。他的著作極大地幫助並影響了後來的深海航海者。墨卡托在盧慰恩大學攻讀了哲學、數學以及天文學。他在那裡還學會了雕刻和製作儀器。他的第一件重要作品是一幅非常詳細的佛蘭德地圖。他的作品質量精絕，當時的皇帝查理五世大加讚賞，委派他製作地球儀。他於1541年完成了這項工作。

佛蘭德後來逐漸變成了一個宗教鬥爭的中心，墨卡托被懷疑是路德教派的信徒，遭到逮捕。出獄后，他搬到了萊茵河畔的大學城——杜伊斯堡。在那裡他成了克利夫斯伯爵的門客，出版了許多地圖，並且繪製出第一張現代歐洲大陸和不列顛島地圖。

墨卡托不久便意識到，世界需要的是一張準確清晰的航海圖。早期的航海家們發現很難將他們的航線畫在圖上，因為地球是圓形的球體，子午線像桔子瓣一樣匯合在南北兩極。那麼怎樣將球面上的一部分繪製在平面上，從而使航海者可以用直線來表示航線呢?

基哈德斯墨卡托找到了答案。他的辦法是把地球表面切成若干份，將每一份展鋪在平面上，然後每一部分好像都有彈力一樣，將它們向兩頭伸拉，直到它們的兩端連在一塊兒。在離南北兩極最近的地方伸拉的幅度最大，因此格陵蘭島會變得碩大無比。而在南北回歸線之間的部分，儘管絕大多數的航海活動都是在這裡進行的，但卻伸拉的幅度最小。這樣做的結果，每一部分都變成了一個長方形，和其它部分拼台起來就形成一幅完整的世界地圖。平行的緯線同平行的經線相互交錯形成了經緯網。這樣一來，航海者就可以在平面上用直線畫出他們的航線圖來了。

1569年，墨卡托出版了他的世界地圖，開創了地理學史上的新篇章。今天，大多數深海航行者依舊使用藉助墨卡托投影畫出來的航海圖。

在地圖製圖生產實踐中，已經出現了許多種投影，為了便於研究和使用，有必要進行適當的分類。

按投影面分類

按投影面的形態不同而劃分的三種投影：圓錐投影、圓柱投影和方位投影，這是我們在製圖過程中經常遇到的三種投影方式：

圓錐投影：可以想象為用一個巨大的圓錐體罩住地球，把地表的位置投影到圓錐面上，然後沿著一條經線將圓錐切開展成平面。圓錐體罩住地球的方式可以有兩種情形：與地球相切（單割線）、與地球相割形成兩條與地球表面相割的割線（雙割線）。

圓柱投影：用一個圓柱體罩住地球，把地表的位置投影到圓體面上，然後將圓體切開展成平面。圓柱投影可以作為圓錐投影的一個特例，即圓錐的頂點延伸到無窮遠。

方位投影：以一個平面作為投影面，切於地球表面，把地表的位置投影到平面上。方位投影也可以作為圓錐投影的一個特例，即圓錐的夾角為180度，圓錐變為平面。

按投影面與地球橢球體的相對位置分類

根據投影面與地球橢球體的相對位置的不同，還可以將投影類型分為正軸投影、斜軸投影和橫軸投影；

正軸投影：投影面的軸（圓錐圓柱的軸線，平面的法線）與地球橢球體的旋轉軸重合。也稱正常位置投影，或稱極投影。

斜軸投影：投影面的軸（圓錐圓柱的軸線，平面的法線）既不與地球橢球體的旋轉軸重合也不與赤道面重合。也稱水平投影。

橫軸投影：投影面的軸（圓錐圓柱的軸線，平面的法線）與地球赤道面重合。也稱赤道投影。

按投影后的幾何變形分類

按照投影后的幾何變形分類可分三類：

等角投影（正形投影）：地面上的任意兩條直線的夾角，在經過地球投影繪製到圖紙上以後，其夾角保持不變。

等面積投影：地面上的一塊面積在經過地球投影繪製到圖紙上以後，面積保持不變。

等距離投影：地面上的兩個點之間的距離，在經過地球投影繪製到圖紙上以後，距離保持不變。

實際上，有許多投影既不能保持等角又不能保持等面積，可以稱之為任意投影。在這類投影中，既有角度變形又有面積變形。

綜上所述，投影名稱可以結合上述三種分類方法（投影面形狀、投影面與地球橢球體的位置、投影后的變形性質）加以命名。如：正軸等角圓錐投影、正軸等角圓柱投影等等。

歷史上也有一些投影是以設計者的名稱命名，他們大都可以歸類到上述的分類中，但也有一些此類投影方法無法按上述方法分類。

經過墨卡托投影后的經線是均勻分佈，在此主要介紹緯度的變換方法。

墨卡托投影把緯度為Φ (-90°<Φ<90°)的點投影到：y = sign(Φ)*ln(tan(45° + abs(Φ/2))

其中：

當Φ<0時，sign(Φ)=-1；

當Φ=0時，sign(Φ)=0；

當Φ>0時，sign(Φ)=1；

abs（Φ）是Φ的絕對值。

這種投影演演算法使得赤道附近的緯線較密，極地附近的緯線較稀。極點被投影到無窮遠，所以這種投影不適合在高緯度地區使用。Google Maps的選取的範圍為 -π

以上知識即可實現編程轉換。

缺點

---

墨卡托投影的地圖最大的缺點就是和現實差別太大，變形非常嚴重。

在墨卡托投影的地圖上，變形最嚴重的就是非洲和格陵蘭島了。地圖上非洲的大小和格陵蘭島差不多大，但如果計算一下的話：非洲面積約是3020萬平方千米，格陵蘭島面積約是217萬平方千米，而3020÷217≈14。也就是說，非洲的面積是格陵蘭島的14倍！

再比如墨卡托投影的地圖上的加拿大，看起來是個瘦瘦的長方形，但實際上，加拿大是個類似正方形的的形狀。它不僅扭曲得不像樣，而且還被放大了好幾倍。在地圖上加拿大的面積大約是美國的三倍，實際上加拿大比美國大不了多少。加拿大的面積是998萬平方千米，美國兩部分合起來約963萬平方千米，998÷963≈1.04。也就是說加拿大與美國的面積差不多。