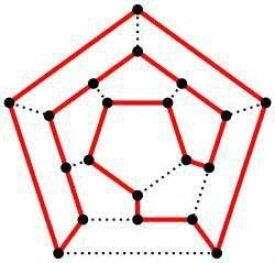
哈密頓迴路
哈密頓提出的數學術語
哈密頓圖(哈密爾頓圖)(英語:Hamiltonian graph,或Traceable graph)是一個無向圖,由天文學家哈密頓提出,由指定的起點前往指定的終點,途中經過所有其他節點且只經過一次。在圖論中是指含有哈密頓迴路的圖,閉合的哈密頓路徑稱作哈密頓迴路(Hamiltonian cycle),含有圖中所有頂點的路徑稱作哈密頓路徑(Hamiltonian path)。
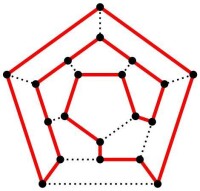
哈密頓迴路
這個問題和著名的七橋問題的不同之處在於,過橋只需要確定起點,而不用確定終點。哈密頓問題尋找一條從給定的起點到給定的終點沿 途恰好經過所有其他城市一次的路徑。
哈密頓路徑問題在上世紀七十年代初,終於被證明是“NP完備”的。據說具有這樣性質的問題,難於找到一個有效的演演算法。實際上對於某些頂點數不到100的網路,利用現有最好的演演算法和計算機也需要比較荒唐的時間(比如幾百年)才能確定其是否存在一條這樣的路徑。
從圖中的任意一點出發,路途中經過圖中每一個結點當且僅當一次,則成為哈密頓迴路。
要滿足兩個條件:
⒈封閉的環
⒉是一個連通圖,且圖中任意兩點可達
經過圖(有向圖或無向圖)中所有頂點一次且僅一次的通路稱為哈密頓通路。
經過圖中所有頂點一次且僅一次的迴路稱為哈密頓迴路。
具有哈密頓迴路的圖稱為哈密頓圖,具有哈密頓通路但不具有哈密頓迴路的圖稱為半哈密頓圖。
平凡圖是哈密頓圖。
⒊若以1到2、2到3、3到4、4到5、5到1,為計數規律,則各點均出現兩次;這種判斷方法在計算機編程運算中顯得尤為重要,其會精簡很多運算過程。
⒋新出爐,有待檢測的代碼如下:
註:這段代碼採用分支定界法作為編寫程序的依據,因此代碼依舊局限在演演算法上;而且代碼的使用對所要計算的數據是有要求的,如下:
⒈只要數據在開始計算出的n個最小值中,其重複次數超過2次的點的種類只能為一種,例如:代碼段中的數據五個最小值中其重複次數超過2次的點只有v5。
⒉數據矩陣格式要求:只允許為上三角矩陣,不支持全矩陣以及下三角矩陣的運算。
⒊代碼擴展方法請使用者獨立思考,不唯一。
⒋運算數據擴展方法,請使用者獨立思考,不唯一。
⒌此代碼為本人畢設的附加產品,不會對使用此代碼者,因理解不當或使用不當而造成的任何不良後果,付出任何責任。
⒍代碼僅供交流。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 | #include #include #include #include #include #include #include #include <cstdlib> #include #include #include #include #define max(a,b) (a>b?a:b) using namespace std; typedef long long(LL); typedef unsigned long long(ULL); const double eps(1e-8); char B[1<<15],*S=B,*T=B,ch; #define getc() (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++) int aa,bb; int F() { while(ch=getc(),(ch<'0'||ch>'9')&&ch!='-'); ch=='-'?aa=bb=0:(aa=ch-'0',bb=1); while(ch=getc(),ch>='0'&&ch<='9')aa=aa*10+ch-'0'; return bb?aa:-aa; } #define N 100010 int n,swp,cnt,z[N]; long long ans; #define swap(a,b) (swp=a,a=b,b=swp) #define abs(x) (x>0?x:-(x)) #define max(a,b) (a>b?a:b) #define cmax(x) (ans struct P {int x,y,id,nx,ny;} p[N]; bool operator<(const P&a,const P&b) {return a.nx class Graph { int et,la[N],ufs[N],tot; struct D { int x,y,v; bool operator<(const D&a)const {return v } d[N<<2]; struct E {int to,v,nxt;} e[N<<1]; int gf(int x) {return ufs[x]==x?x:ufs[x]=gf(ufs[x]);} { e[++et]=(E) {y,v,la[x]},la[x]=et; e[++et]=(E) {x,v,la[y]},la[y]=et; } public: Graph() {et=1;} void add(int x,int y,int v) {d[++tot]=(D) {x,y,v};} void make() { std::sort(d+1,d+1+tot); for(int i=1; i<=n; i++)ufs[i]=i; cnt=n; for(int i=1,x,y; i<=tot; i++) if((x=gf(d[i].x))!=(y=gf(d[i].y))) { ufs[x]=y,cnt--,ans+=d[i].v, adde(d[i].x,d[i].y,d[i].v); } } } G; struct D {int x,n;} d[N]; bool operator<(const D&a,const D&b) {return a.x #define dis(i,j) (abs(p[i].x-p[j].x)+abs(p[i].y-p[j].y)) void ins(int i) { for(int t=p[i].ny; t<=cnt; t+=t&-t) if(z[t]==0||p[z[t]].x+p[z[t]].y } int query(int i) { int f=0; for(int t=p[i].ny; t>0; t-=t&-t) if(z[t]&&(f==0||p[z[t]].x+p[z[t]].y>p[f].x+p[f].y))f=z[t]; return f; } void work() { for(int i=1; i<=n; i++)p[i].nx=p[i].x-p[i].y,p[i].ny=p[i].y; std::sort(p+1,p+1+n); for(int i=1; i<=n; i++)d[i]=(D) {p[i].ny,i}; std::sort(d+1,d+1+n); d[n+1].x=d[n].x; cnt=1; for(int i=1; i<=n; i++) { p[d[i].n].ny=cnt; if(d[i].x!=d[i+1].x)cnt++; } memset(z,0,sizeof(z)); for(int i=1,j; i<=n; ins(i++)) if(j=query(i))G.add(p[i].id,p[j].id,dis(i,j)); } int main() { n=F(); for(int i=1; i<=n; i++)p[i]=(P) {F(),F(),i}; work(); for(int i=1; i<=n; i++)swap(p[i].x,p[i].y); work(); for(int i=1; i<=n; i++)p[i].y=-p[i].y; work(); for(int i=1; i<=n; i++)swap(p[i].x,p[i].y); work(); G.make(); printf("%lld\n",ans); } |