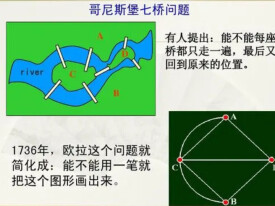
七橋問題
數學問題
1736年29歲的歐拉向聖彼得堡科學院遞交了《哥尼斯堡的七座橋》的論文,在解答問題的同時,開創了數學的一個新的分支——圖論與幾何拓撲,也由此展開了數學史上的新曆程。
七橋問題提出后,很多人對此很感興趣,紛紛進行試驗,但在相當長的時間裡,始終未能解決。歐拉通過對七橋問題的研究,不僅圓滿地回答了哥尼斯堡居民提出的問題,而且得到並證明了更為廣泛的有關一筆畫的三條結論,人們通常稱之為“歐拉定理F”。
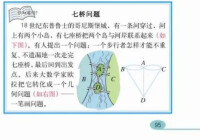
七橋問題
有關圖論研究的熱點問題。18世紀初普魯士的哥尼斯堡,有一條河穿過,河上有兩個小島,有七座橋把兩個島與河岸聯繫起來(如右上圖)。有個人提出一個問題:一個步行者怎樣才能不重複、不遺漏地一次走完七座橋,最後回到出發點。後來大數學家歐拉把它轉化成一個幾何問題(如左圖下)——一筆畫問題。他不僅解決了此問題,且給出了連通圖可以一筆畫的充要條件是:奇點的數目不是0 個就是2 個(連到一點的數目如是奇數條,就稱為奇點,如果是偶數條就稱為偶點,要想一筆畫成,必須中間點均是偶點,也就是有來路必有另一條去路,奇點只可能在兩端,因此任何圖能一筆畫成,奇點要麼沒有要麼在兩端) 。
當Euler在1736年訪問Konigsberg, Prussia(now Kaliningrad Russia)時,他發現當地的市民正從事一項非常有趣的消遣活動。Konigsberg城中有一條名叫Pregel的河流橫經其中,這項有趣的消遣活動是在星期六作一次走過所有七座橋的散步,每座橋只能經過一次而且起點與終點必須是同一地點。
Euler把每一塊陸地考慮成一個點,連接兩塊陸地的橋以線表示。
後來推論出此種走法是不可能的。他的論點是這樣的,除了起點以外,每一次當一個人由一座橋進入一塊陸地(或點)時,他(或她)同時也由另一座橋離開此點。所以每行經一點時,計算兩座橋(或線),從起點離開的線與最後回到始點的線亦計算兩座橋,因此每一個陸地與其他陸地連接的橋數必為偶數。

著名數學家歐拉的畫像
歐拉的這個考慮非常重要,也非常巧妙,它正表明了數學家處理實際問題的獨特之處——把一個實際問題抽象成合適的“數學模型”。這種研究方法就是“數學模型方法”。這並不需要運用多麼深奧的理論,但想到這一點,卻是解決難題的關鍵。
接下來,歐拉運用圖中的一筆畫定理為判斷準則,很快地就判斷出要一次不重複走遍哥尼斯堡的7座橋是不可能的。也就是說,多少年來,人們費腦費力尋找的那種不重複的路線,根本就不存在。一個曾難住了那麼多人的問題,竟是這麼一個出人意料的答案!
問題初期
問題提出后,很多人對此很感興趣,紛紛進行試驗,但在相當長的時間裡,始終未能解決。而利用普通數學知識,每座橋均走一次,那這七座橋所有的走法一共有5040種,而這麼多情況,要一一試驗,這將會是很大的工作量。但怎麼才能找到成功走過每座橋而不重複的路線呢?因而形成了著名的“哥尼斯堡七橋問題”。
問題後期進展
1735年,有幾名大學生寫信給當時正在俄羅斯的彼得斯堡科學院任職的天才數學家歐拉,請他幫忙解決這一問題。歐拉在親自觀察了哥尼斯堡七橋后,認真思考走法,但始終沒能成功,於是他懷疑七橋問題是不是原本就無解呢?
1736年,在經過一年的研究之後,29歲的歐拉提交了《哥尼斯堡七橋》的論文,圓滿解決了這一問題,同時開創了數學新一分支---圖論。
在論文中,歐拉將七橋問題抽象出來,把每一塊陸地考慮成一個點,連接兩塊陸地的橋以線表示。並由此得到了如圖一樣的幾何圖形。若我們分別用A、B、C、D四個點表示為哥尼斯堡的四個區域。這樣著名的“七橋問題”便轉化為是否能夠用一筆不重複的畫出過此七條線的問題了。若可以畫出來,則圖形中必有終點和起點,並且起點和終點應該是同一點,由於對稱性可知由B或C為起點得到的效果是一樣的,若假設以A為起點和終點,則必有一離開線和對應的進入線,若我們定義進入A的線的條數為入度,離開線的條數為出度,與A有關的線的條數為A的度,則A的出度和入度是相等的,即A的度應該為偶數。即要使得從A出發有解則A的度數應該為偶數,而實際上A的度數是5為奇數,於是可知從A出發是無解的。同時若從B或D出發,由於B、D的度數分別是3、3,都是奇數,即以之為起點都是無解的。
七橋問題
由此我們得到:歐拉迴路關係
由此我們可知要使得一個圖形可以一筆畫,必須滿足如下兩個條件:
1. 圖形必須是連通的。
2. 圖中的“奇點”個數是0或2。
我們也可以依此來檢驗圖形是不是可一筆畫出。回頭也可以由此來判斷“七橋問題”,4個點全是奇點,可知圖不能“一筆畫出”,也就是不存在不重複地通過所有七橋。
1736年,歐拉在交給彼得堡科學院的《哥尼斯堡7座橋》的論文報告中,闡述了他的解題方法。他的巧解,為後來的數學新分支——拓撲學的建立奠定了基礎。
七橋問題和歐拉定理
歐拉通過對七橋問題的研究,不僅圓滿地回答了哥尼斯堡居民提出的問題,而且得到並證明了更為廣泛的有關一筆畫的三條結論,人們通常稱之為 歐拉定理。對於一個連通圖,通常把從某結點出發一筆畫成所經過的路線叫做歐拉路。人們又通常把一筆畫成回到出發點的歐拉路叫做歐拉迴路。具有歐拉迴路的圖叫做歐拉圖。
此題被人教版小學數學第十二冊書收錄.104頁。
此題也被人教版初中第一冊收錄.在121頁。
一筆畫
⒈凡是由偶點組成的連通圖,一定可以一筆畫成。畫時可以把任一偶點為起點,最後一定能以這個點為終點畫完此圖。
⒉凡是只有兩個奇點的連通圖(其餘都為偶點),一定可以一筆畫成。畫時必須把一個奇點為起點,另一個奇點為終點。
⒊其他情況的圖都不能一筆畫出。(奇點數除以二便可算出此圖需幾筆畫成。)