歐拉定理
數學世界中最美妙的定理
在數學及許多分支中都可以見到很多以歐拉命名的常數、公式和定理。在數論中,歐拉定理(Euler Theorem,也稱費馬-歐拉定理或歐拉函數定理)是一個關於同餘的性質。歐拉定理得名於瑞士數學家萊昂哈德·歐拉,該定理被認為是數學世界中最美妙的定理之一。歐拉定理實際上是費馬小定理的推廣。此外還有平面幾何中的歐拉定理、多面體歐拉定理(在一凸多面體中,頂點數-棱邊數+面數=2)。
西方經濟學中歐拉定理又稱為產量分配凈盡定理,指在完全競爭的條件下,假設長期中規模收益不變,則全部產品正好足夠分配給各個要素。另有歐拉公式。
萊昂哈德·歐拉(Leonhard Euler ,1707年4月15日~1783年9月18日),瑞士數學家,13歲進巴塞爾大學讀書,得到著名數學家貝努利的精心指導.歐拉是科學史上最多產的一位傑出的數學家,他從19歲開始發表論文,直到76歲,他那不倦的一生,共寫下了886本書籍和論文,其中在世時發表了700多篇論文。彼得堡科學院為了整理他的著作,整整用了47年。歐拉著作驚人的高產並不是偶然的。他那頑強的毅力和孜孜不倦的治學精神,可以使他在任何不良的環境中工作:他常常抱著孩子在膝蓋上完成論文。即使在他雙目失明后的17年間,也沒有停止對數學的研究,口述了好幾本書和400餘篇的論文。當他寫出了計算天王星軌道的計算要領后離開了人世。歐拉永遠是我們可敬的老師。歐拉研究論著幾乎涉及到所有數學分支,對物理力學、天文學、彈道學、航海學、建築學、音樂都有研究!有許多公式、定理、解法、函數、方程、常數等是以歐拉名字命名的。歐拉寫的數學教材在當時一直被當作標準教程。19世紀偉大的數學家高斯(Gauss,1777-1855)曾說過“研究歐拉的著作永遠是了解數學的最好方法”。歐拉還是數學符號發明者,他創設的許多數學符號,例如π,i,e,sin,cos,tg,Σ,f (x)等等,至今沿用。歐拉不僅解決了彗星軌跡的計算問題,還解決了使牛頓頭痛的月地問題。對著名的“哥尼斯堡七橋問題”的完美解答開創了“圖論”的研究。歐拉發現,不論什麼形狀的凸多面體,其頂點數V、棱數E、面數F之間總有關係V+F-E=2,此式稱為歐拉公式。V+F-E即歐拉示性數,已成為“拓撲學”的基礎概念。
在數論中,歐拉定理,(也稱 費馬-歐拉定理)是一個關於同餘的性質。歐拉定理表明,若n,a為正整數,且n,a互質,則:
將1~n中與n互質的數按順序排布:x1,x2……xφ(n) (顯然,共有φ(n)個數)
我們考慮這麼一些數:
m1=a*x1;m2=a*x2;m3=a*x3……mφ(n)=a*xφ(n)
1)這些數中的任意兩個都不模n同餘,因為如果有mS≡mR (mod n) (這裡假定mS更大一些),就有:
mS-mR=a(xS-xR)=qn,即n能整除a(xS-xR)。但是a與n互質,a與n的最大公因子是1,而xS-xR


 V+F-E=X(P),V是多面體P的頂點個數,F是多面體P的面數,E是多面體P的棱的條數,X(P)是多面體P的歐拉示性數。
V+F-E=X(P),V是多面體P的頂點個數,F是多面體P的面數,E是多面體P的棱的條數,X(P)是多面體P的歐拉示性數。
 對 的邊數用數學歸納法.
對 的邊數用數學歸納法.
2)這些數除n的餘數都與n互質,因為如果餘數與n有公因子r,那麼a*xi=pn+qr=r(……),a*xi與n不互質,而這是不可能的。(因為a*xi=pn+qr=r(……),說明a*xi含有因子r,又因為前面假設n含有因子r,所以a*xi和n含有公因子r,因此a*xi與n不互質)那麼這些數除n的餘數,都在x1,x2,x3……xφ(n)中,因為這是1~n中與n互質的所有數,而餘數又小於n.
由1)和2)可知,數m1,m2,m3……mφ(n)(如果將其次序重新排列)必須相應地同餘於x1,x2,x3……xφ(n).
故得出:m1*m2*m3……mφ(n)≡x1*x2*x3……xφ(n) (mod n)
或者說a^[φ(n)]*(x1*x2*x3……xφ(n))≡x1*x2*x3……xφ(n)
或者為了方便:K{a^[φ(n)]-1}≡0 ( mod n ) 這裡K=x1*x2*x3……xφ(n)。
可知K{a^[φ(n)]-1}被n整除。但K中的因子x1,x2……都與n互質,所以K與n互質。那麼a^[φ(n)]-1必須能被n整除,即a^[φ(n)]-1≡0 (mod n),即a^[φ(n)]≡1 (mod n),得證。
費馬小定理:
a是不能被質數p整除的正整數,則有a^(p-1) ≡ 1 (mod p)
證明這個定理非常簡單,由於p是質數,所以有φ(p) = p-1,代入歐拉定理即可證明。推論:對於任意正整數a,有a^p ≡ a (mod p),因為a能被p整除時結論顯然成立。
首先看一個基本的例子。令a = 3,n = 5,這兩個數是互素的。比5小的正整數中與5互素的數有1、2、3和4,所以φ(5)=4(詳情見[歐拉函數])。計算:a^{φ(n)} = 3^4 =81,而81= 80 + 1 Ξ 1 (mod 5)。與定理結果相符。
這個定理可以用來簡化冪的模運算。比如計算7^{222}的個位數,實際是求7^{222}被10除的餘數。7和10[[互素]],且φ(10)=4。由歐拉定理知7^4Ξ1(mod 10)。所以7^{222}=(7^4)^55*(7^2)Ξ1^{55}*7^2Ξ49Ξ9 (mod 10)。
1)設三角形的外接圓半徑為R,內切圓半徑為r,外心與內心的距離為d,則d^2=R^2-2Rr.
2)三角形ABC的垂心H,九點圓圓心V,重心G,外心O共線,稱為 歐拉線
1)證明過程見下圖:
2)證明過程見下圖

合併圖冊

歐拉定理

歐拉定理

合併圖冊
如果P可以同胚於一個球面(可以通俗地理解為能吹脹成一個球面),那麼X(P)=2,如果P同胚於一個接有h個環柄的球面,那麼X(P)=2-2h。
X(P)叫做P的拓撲不變數,是拓撲學研究的範圍。
歐拉定理
歐拉定理
歐拉定理
如果一個聯通平面圖 有 個頂點、條邊、個面,那麼
歐拉定理
歐拉定理
若 只有一個頂點,則, , ,故 成立.
歐拉定理
若 為一條邊,則, , ,故 成立.
歐拉定理
若 增加一條邊,則 成立.
歐拉定理
若 增加一個頂點,則 成立.
按照數學歸納法原理,定理對於任何聯通平面圖成立.
歐拉定理指出:如果產品市場和要素市場都是完全競爭的,而且廠商生產的規模報酬不變,那麼在市場均衡的條件下,所有生產要素實際所取得的報酬總量正好等於社會所生產的總產品。該定理又叫做邊際生產力分配理論,還被稱為產品分配凈盡定理。如上所述,要素的價格是由於要素的市場供給和市場需求共同決定。在完全競爭的條件下,廠商和消費者都被動地接受市場形成的價格。
在完全競爭的條件下,廠商使用要素的原則是:要素的邊際產品價值等於要素價格。即:
P*MPL=W (1)
P*MPK=r (2)
由式1和2可得:
MPL=W/P (3)
MPK=r/p(4
P為產品的價格,W/P和r/P分別表示了勞動力和資本的實際報酬。因為在完全競爭的條件下,單位勞動、單位資本的實際報酬分別等於勞動、資本的邊際產量。假定整個社會的勞動總量和資本總量為L和K,而社會總產品為Q,又在市場均衡的條件下,所有生產要素實際所取得的報酬總量正好等於社會所生產的總產品,得:
Q=L*MPL+K*MPK(5)
式5稱為歐拉分配定理。它是由於該定理的證明使用了數學上的歐拉定理而得名。
假設生產函數為:Q=f(L.K)(即Q為齊次生產函數),定義人均資本k=K/L
方法1:根據齊次生產函數中不同類型的生產函數進行分類討論
(1)線性齊次生產函數
n=1,規模報酬不變,因此有:
Q/L=f(L/L,K/L)=f(1,k)=g(k)
k為人均資本,Q/L為人均產量,人均產量是人均資本k的函數。
讓Q對L和K求偏導數,有:
∂Q/∂L=∂[L*g(k)]/∂L=g(k)+L*[dg(k)/dk]*[dk/dL]=g(k)+L*g’(k)*(-K/ )=g(k)-k*g’(k)
∂Q/∂K=∂[L*g(k)]/ ∂K=L*[∂g(k)/∂k]=L*[dg(k)/dk]*[∂k/∂K]=L*g’(k)*(1/L)=g’(k)
由上面兩式,即可得歐拉分配定理:
L*[∂Q/∂L]+K*[∂Q/∂K]=L*[g(k)-k*g’(k)]+K*g’(k)=L*g(k)-K*g’(k)+K*g’(k)=L*g(k)=Q
(2)非線性齊次生產函數
1.當n〉1時,規模報酬遞增,如果按照邊際生產力分配,則產品不夠分配給各個生產要素,即:
L*[∂Q/∂L]+K*[∂Q/∂K]>Q
2.當n<1時,規模報酬遞減,如果按邊際生產力進行分配,則產品在分配給各個生產要素之後還有剩餘,即:
L*[∂Q/∂L]+K*[∂Q/∂K]
方法2:設一個一般的齊次生產函數Q=f(L,K)為n齊次(即n任意的齊次生產函數,既可以是線性的,也可以是非線性的),則有:
Q=L *g(k)
將該函數對K,對L求偏導數,得:
∂Q/∂K=g’(k)
∂Q/∂L=ng(k)-kg’(k)
綜合上述兩式,有:
L*(∂Q/∂L)+K*(∂Q/∂K)=nL*g(k)=nQ
當n=1時,規模報酬不變,該式即為歐拉分配定理
當n〉1時,規模報酬遞增,故有:
L*[∂Q/∂L]+K*[∂Q/∂K]>Q
當n<1時,規模報酬遞減,故有:
L*[∂Q/∂L]+K*[∂Q/∂K]
 嘗試一下用拓撲學方法證明關於多面體的面、棱、頂點數的歐拉公式。
嘗試一下用拓撲學方法證明關於多面體的面、棱、頂點數的歐拉公式。
在技術經濟學中,歐拉定理屬於一次齊次函數的一個重要性質,它是說一次齊次函數的數值都可以表示為各自變數和因變數對相應自變數一階偏導的乘積之和。在理論上,這句話顯得很晦澀,可以用一個很形象的例子來解釋。
假設有兩個人,他們一個有十個胡蘿蔔的種子,另外一個有種胡蘿蔔的經驗,他們打算合作,前者出種子,後者出勞力,用十天的時間來種植胡蘿蔔。在這過程中,風調雨順,沒有什麼意外,種子全部茁壯成長,擁有種植經驗的人也盡職盡責,最後得到的胡蘿蔔的產量是最大化的,有十公斤。而每個種子的在自然狀態下能產出0.5公斤的胡蘿蔔,勞動者每一天能辛勞能使胡蘿蔔在最終增加0.5公斤,所以最後的產量也是10=0.5*10+0.5*10,即種子(資本)的邊際產出乘以資本量加上勞動的邊際產出乘以勞動量等於總產出。
上邊是對歐拉定理在經濟學中一次齊次生產函數的解釋。但是它又有什麼深刻的含義呢?在宏觀經濟中,上述的歐拉定理可以被解釋為收入的分配,也就是在胡蘿蔔的例子中,前五公斤的蘿蔔是由資本所作出的貢獻,后五公斤是由勞動所作出的貢獻,如果社會這種很理想量化的貢獻來分配產出,那麼社會的分配是公平也富有效率的,也是能夠自動將產出出清的。
這樣看來,一個社會的產出如果能用歐拉定理將各種生產要素的貢獻清晰量化,按貢獻分配產出,那麼這個社會是如此的美好啊,至少每個勞動者,每個資本擁有者用了生產的動力,不會像人民公社中的按需分配的成員那樣隨處搭便車,產生囚徒困境的窘境,也不會像如今這樣勞動者到處訴苦說自己的貢獻在社會分配中被低估,而國家有制定最低工資制度,結果造成在位者的得利,失業者的痛苦。
也有人一定會指責歐拉定理的理想狀態,肯定會說,這樣的話整個社會的產出就被當期消費掉了,沒有留下盈餘成為資本來在將來擴大再生產,我們的後代怎麼辦?餓肚子么?其實這個問題也是值得考慮的,吃光了的,甚至把種子都吃了,將來當然會一命嗚呼,但是盈餘讓勞動者,資本所有者們在當期享樂,總比把當期的盈餘變成各種“白宮”好吧?
定理內容
歐拉定理
e^(ix)=cosx+isinx
e是自然對數的底,i是虛數單位。
將公式里的x換成-x,得到:
e^(-ix)=cosx-isinx,然後採用兩式相加減的方法得到:
sinx=[e^(ix)-e^(-ix)]/(2i),cosx=[e^(ix)+e^(-ix)]/2.
這兩個也叫做歐拉公式。
上帝創造的公式
將e^(ix)=cosx+isinx中的x取作π就得到:
e^(iπ)+1=0.
這個等式也叫做歐拉公式,它是數學里最令人著迷的一個公式,它將數學里最重要的幾個數字聯繫到了一起:兩個超越數:自然對數的底e,圓周率π,兩個單位:虛數單位i和自然數的單位1,以及數學里常見的0。數學家們評價它是“上帝創造的公式”,我們只能看它而不能理解它。
1.數學規律:公式描述了簡單多面體中頂點數、面數、棱數之間特有的規律
2.思想方法創新:定理髮現證明過程中,觀念上,假設它的表面是橡皮薄膜製成的,可隨意拉伸;方法上將底面剪掉,化為平面圖形(立體圖→平面拉開圖)。
3.引入拓撲學:從立體圖到拉開圖,各面的形狀、長度、距離、面積等與度量有關的量發生了變化,而頂點數,面數,棱數等不變。
定理引導我們進入一個新幾何學領域:拓撲學。我們用一種可隨意變形但不得撕破或粘連的材料(如橡皮波)做成的圖形,拓撲學就是研究圖形在這種變形過程中的不變的性質。
4.提出多面體分類方法:
在歐拉公式中, f (p)=V+F-E 叫做歐拉示性數。歐拉定理告訴我們,簡單多面體f (p)=2。
除簡單多面體外,還有非簡單多面體。例如,將長方體挖去一個洞,連接底面相應頂點得到的多面體。它的表面不能經過連續變形變為一個球面,而能變為一個環面。其歐拉示性數f (p)=16+16-32=0,即帶一個洞的多面體的歐拉示性數為0。
5.利用歐拉定理可解決一些實際問題
如:為什麼正多面體只有5種?足球與C60的關係?否有棱數為7的正多面體?等
逐步減少多面體的棱數,分析V+F-E
先以簡單的四面體ABCD為例分析證法。
去掉一個面,使它變為平面圖形,四面體頂點數V、棱數E與剩下的面數F1變形后都沒有變。因此,要研究V、E和F關係,只需去掉一個面變為平面圖形,證V+F1-E=1
1.去掉一條棱,就減少一個面,V+F1-E不變。依次去掉所有的面,變為“樹枝形”。
2.從剩下的樹枝形中,每去掉一條棱,就減少一個頂點,V+F1-E不變,直至只剩下一個點。
以上過程V+F1-E不變,V+F1-E=1,所以加上去掉的一個面,V+F-E =2。
對任意的簡單多面體,運用這樣的方法,都是只剩下一條線段。因此公式對任意簡單多面體都是正確的。
計算多面體各面內角和
設多面體頂點數V,面數F,棱數E。剪掉一個面,使它變為平面圖形(拉開圖),求所有面內角總和Σα
一方面,在原圖中利用各面求內角總和。
設有F個面,各面的邊數為n1,n2,…,nF,各面內角總和為:
Σα = [(n1-2)·180度+(n2-2)·180度+…+(nF-2) ·180度]
= (n1+n2+…+nF -2F) ·180度
=(2E-2F) ·180度 = (E-F) ·360度(1)
另一方面,在拉開圖中利用頂點求內角總和。
設剪去的一個面為n邊形,其內角和為(n-2)·180角,則所有V個頂點中,有n個頂點在邊上,V-n個頂點在中間。中間V-n個頂點處的內角和為(V-n)·360度,邊上的n個頂點處的內角和(n-2)·180度。
所以,多面體各面的內角總和:
Σα = (V-n)·360度+(n-2)·180度+(n-2)·180度
=(V-2)·360度(2)
由(1)(2)得:(E-F) ·360度=(V-2)·360度
所以 V+F-E=2.
用拓撲學方法證明

圖
歐拉公式:對於任意多面體(即各面都是平面多邊形並且沒有洞的立體),假設F,E和V分別表示面,棱(或邊),角(或頂)的個數,那末
F-E+V=2。
證明 如圖(圖是立方體,但證明是一般的,是“拓樸”的):
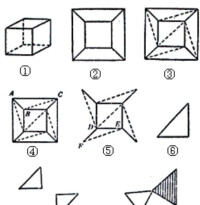
1.把多面體(圖中①)看成表面是薄橡皮的中空立體。
2.去掉多面體的一個面,就可以完全拉開鋪在平面上而得到一個平面中的直線形,像圖中②的樣子。假設F′,E′和V′分別表示這個平面圖形的(簡單)多邊形、邊和頂點的個數,我們只須證明F′-E′+V′=1。
3.對於這個平面圖形,進行三角形分割,也就是說,對於還不是三角形的多邊形陸續引進對角線,一直到成為一些三角形為止,像圖中③的樣子。每引進一條對角線,F′和E′各增加1,而V′卻不變,所以F′-E′+V′不變。因此當完全分割成三角形的時候,F′-E′+V′的值仍然沒有變。有些三角形有一邊或兩邊在平面圖形的邊界上。
4.如果某一個三角形有一邊在邊界上,例如圖④中的△ABC,去掉這個三角形的不屬於其他三角形的邊,即AC,這樣也就去掉了△ABC。這樣F′和E′各減去1而V′不變,所以F′-E′+V′也沒有變。
5.如果某一個三角形有二邊在邊界上,例如圖⑤中的△DEF,去掉這個三角形的不屬於其他三角形的邊,即DF和EF,這樣就去掉△DEF。這樣F′減去1,E′減去2,V′減去1,因此F′-E′+V′仍沒有變。
6.這樣繼續進行,直到只剩下一個三角形為止,像圖中⑥的樣子。這時F′=1,E′=3,V′=3,因此F′-E′+V′=1-3+3=1。
7.因為原來圖形是連在一起的,中間引進的各種變化也不破壞這事實,因此最後圖形還是連在一起的,所以最後不會是分散在向外的幾個三角形,像圖中⑦那樣。
8.如果最後是像圖中⑧的樣子,我們可以去掉其中的一個三角形,也就是去掉1個三角形,3個邊和2個頂點。因此F′-E′+V′仍然沒有變。
即F′-E′+V′=1
成立,於是歐拉公式:F-E+V=2 得證。
例:足球表面由五邊形和六邊形的皮革拼成,計算一共有多少個這樣的五邊形和六邊形?
答:足球是多面體,滿足歐拉公式F-E+V=2,其中F,E,V分別表示面,棱,頂點的個數
設足球表面正五邊形(黑皮子)和正六邊形(白皮子)的面各有x個和y個,那麼
面數F=x+y
棱數E=(5x+6y)/2(每條棱由兩塊皮子共用)
頂點數V=(5x+6y)/3(每個頂點由三塊皮子共用)
由歐拉公式,x+y-(5x+6y)/2+(5x+6y)/3=2,
解得x=12。所以,共有12塊黑皮子
所以,黑皮子一共有12×5=60條棱,這60條棱都是與白皮子縫合在一起的
對於白皮子來說:每塊白色皮子的6條邊中,有3條邊與黑色皮子的邊縫在一起,另3條邊則與其它白色皮子的邊縫在一起。
所以白皮子所有邊的一半是與黑皮子縫合在一起的
那麼白皮子就應該一共有60×2=120條邊,120÷6=20
所以共有20塊白皮子
(或者,每一個六邊形的六條邊都與其它的三個六邊形的三條邊和三個五邊形的三條邊連接;每一個五邊形的五條邊都與其它的五個六邊形的五條邊連接
所以,五邊形的個數x=3y/5。
之前求得x=12,所以y=20)
a^r/(a-b)(a-c)+b^r/(b-c)(b-a)+c^r/(c-a)(c-b)
當r=0,1時式子的值為0
當r=2時值為1
當r=3時值為a+b+c
當r=4時值為a^2+b^2+c^2+ab+bc+ca
r=5時值為a^3+b^3+c^3+ab(a+b)+bc(b+c)+ca(c+a)+abc
一般的,當r取正整數n時,有a^n/(a-b)(a-c)+b^n/(b-c)(b-a)+c^n/(c-a)(c-b) =∑ (a^i)*(b^j)*(c^k),
其中i,j,k是非負整數,且i+j+k=n-2。
由e^iθ=cosθ+isinθ,得到:
sinθ=(e^iθ-e^-iθ)/2i
cosθ=(e^iθ+e^-iθ)/2
設R為三角形外接圓半徑,r為內切圓半徑,d為外心到內心的距離,則:
d^2=R^2-2Rr
設v為頂點數,e為棱數,f是面數,則
v-e+f=2-2p
p為歐拉示性數,例如
p=0 的多面體叫第零類多面體
p=1 的多面體叫第一類多面體
設一個二維幾何圖形的頂點數為V,劃分區域數為Ar,一筆畫筆數為B,則有:
V+Ar-B=1
(如:矩形加上兩條對角線所組成的圖形,V=5,Ar=4,B=8)定理內容
在同一個三角形中,它的外心Circumcenter、重心Gravity、九點圓圓心Nine-point-center、垂心Orthocenter共線。
其實歐拉公式是有很多的,上面僅是幾個常用的。
歐拉定理 若(a,n)=1,則aφ(n)≡1 (mod n) 其中n是正整數,φ(n)是小於n且與n互素的正整數的個數,稱歐拉函數。證:設R={x1,x2,...,xφ(n)}是由小於n且與n互素的全體數組成的集合,a╳R={ax1 mod n,ax2 mod n,...,axφ(n) mod n}},對a╳R中任一元素axi mod n,因a與n互素,xi與n互素,所以axi與n互素①②,又axi mod n
所以aφ(n)≡1 (mod n)。 ①(A)設a,b和c是正整數,(a,b)=1,a|bc,則a|c。(涉最小公倍數證明從略) (B)設a,b和c是正整數,(a,b)=1,c|a,則(b,c)=1。證:設(b,c)=d且d>1,則有d|b,d|c。由d|c,c|a,⇒d|a。由於d|a,d|b,所以d是a和b的公因數,而a,b的最大公因數(a,b)=1,與定義矛盾,因此(b,c)=1。 (C)設a,b和c是正整數,(a,b)=1,則(a,bc)=(a,c)。證:設(a,c)=d1,(a,bc)=d2,一方面d1|a,d1|c,d2|a,d2|bc,⇒d1|a,d1|bc,⇒d1是a和bc的公因數,依定義:d1≤d2 另方面由d2|a,(a,b)=1及性質(7)得(d2,b)=1。從(d2,b)=1,d2|bc,由性質(6)得d2|c,⇒d2是a和c的公因數,依定義:d2≤d1 從而d2=d1,故(a,c)=(a,bc)。推論:若(a,b)=(a,c)=1,則(a,bc)=1。 ②根據性質gad(a,b)=gad(b,r),有(a,n)=(axi mod n,n)=1。 ③設axi mod n=axj mod n,1≢xi,xj≢n.⇔axi≡axj(mod n),由a與n互素知,a在mod n下有乘法逆元或消去律,⇔xi≡xj(mod n),⇔xi mod n≡xj mod n,記xi=nq1+r,xj=nq2+r,⇒xi-xj=n(q2-q1)⇒xi=xj+n(q2-q1),若q2≠q1⇒xi>n,所以xi=xj。 ④[(a mod m)╳(b mod m)]mod m=(a╳b) mod m ∏(axi mod n)=∏xi,∏axi≡∏xi( mod n),aφ(n) ∏xi≡∏xi( mod n)。④ i=1 φ(n) i=1 i=1 i=1 i=1 i=1 φ(n) φ(n) φ(n) φ(n) φ(n) 由每一xi與n互素,知∏xi與n互素,∏xi在mod n下有乘法逆元。 i=1 i=1 φ(n) φ(n)
2011年~2012學年第一學期 密碼學基礎 網路工程0901-0902 開課時間:2011-08
《現代密碼學》,楊波,清華大學出版社,2007年4月 第4章公鑰密碼-歐拉定理 證 (a╳b) mod m=(jm+ra)╳(km+rb)mod m=((jkm+kra+jrb)m+rarb) mod m=(rarb) mod m=[(a mod m)╳(b mod m)]mod m。費爾瑪定理 若p是素數,a正整數,且(a,p)=1,則ap-1≡1(mod n) 證:歐拉定理取n為素數p,歐拉函數φ(p)=p-1,即得費爾瑪定理。
目錄
