外心

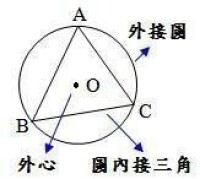
數學名詞。指三角形三條邊的垂直平分線（中垂線）的相交點。用這個點做圓心可以畫三角形的外接圓。指三角形外接圓的圓心，一般叫三角形的外心。三角形的外心是三邊中垂線的交點，且這點到三角形三頂點的距離相等。外心是三角形三條邊的垂直平分線的交點，即外接圓的圓心。

外心定理：三角形的三邊的垂直平分線交於一點。該點叫做三角形的。證明注意到外心到三角形的三個頂點距離相等，結合垂直平分線定義，外心定理其實極好證。計算外心的重心坐標是一件麻煩的事。先計算下列臨時變數：d1,d2,d3分別是三角形三個頂點連向另外兩個頂點向量的點乘。c1=d2d3，c2=d1d3，c3=d1d2；c=c1+c2+c3。重心坐標：( (c2+c3)/2c，(c1+c3)/2c，(c1+c2)/2c )。且：直角三角形外心在斜邊的中點。銳角三角形外心在內部。鈍角三角形外心在外部。設O是三角形ABC的外心則∠AOC=2∠ABC,∠AOB=2∠ACB與多邊形各角都相交的圓叫做多邊型的外接圓。三角形一定有外接圓，其他的圖形不一定有外接圓。三角形的外接圓圓心是三條中垂線的交點，直角三角形的外接圓圓心在斜邊的中點上。三角形外接圓圓心叫外心有外心的圖形，一定有外接圓(各邊中垂線的交點，叫做外心）例題分析例1 如圖1-125，PC⊥平面ABC，AB=BC=CA=PC，求二面角B－PA－C的平面角的正切值．分析 由PC⊥平面ABC，知平面ABC⊥平面PAC，從而B在平面PAC上的射影在AC上，由此可用三垂線定理作出二面角的平面角．解 ∵ PC⊥平面ABC∴ 平面PAC⊥平面ABC，交線為AC作BD⊥AC於D點，據面面垂直性質定理，BD⊥平面PAC，作DE⊥PA於E，連BE，據三垂線定理，則BE⊥PA，從而∠BED是二面角B－PA－C的平面角．設PC=a，依題意知三角形ABC是邊長為a的正三角形，∴ D是∵PC = CA=a，∠PCA=90°，∴ ∠PAC=45°∴ 在Rt△DEA評註 本題解法使用了三垂線定理來作出二面角的平面角后，再用解三角形的方法來求解．例2 在60°二面角M－a－N內有一點P，P到平面M、平面N的距離分別為1和2，求點P到直線a的距離．(圖1－126)分析 設PA、PB分別為點P到平面M、N的距離，過PA、PB作平面α，分別交M、N於AQ、BQ．同理，有PB⊥a，∵ PA∩PB=P，∴ a⊥面PAQB於Q又 AQ、BQ平面PAQB∴ AQ⊥a，BQ⊥a．∴ ∠AQB是二面角M－a－N的平面角．∴ ∠AQB=60°連PQ，則PQ是P到a的距離，在平面圖形PAQB中，有∠PAQ=∠PBQ=90°∴ P、A、Q、B四點共圓，且PQ是四邊形PAQB的外接圓的直徑2R在△PAB中，∵ PA=1，PB=2，∠BPA=180°-60°=120°，由余弦定理得AB2=1+4-2×1×2cos120°=7由正弦定理：評註 本例題中，通過作二面角的棱的垂面，找到二面角的平面角．例3 如圖1-127過正方形ABCD的頂點A作PA⊥平面ABCD，設PA=AB=a 求(1)二面角B－PC－D的大小；(2)平面PAB和平面PCD所成二面角的大小．分析 二面角B－PC－D的棱為PC，所以找平面角作棱的垂線，而平面PAB和平面PCD所成二面角“無棱”須找二面角的棱．解 (1)∵ PA⊥平面ABCD，BD⊥AC∴ BD⊥PC(三垂線定理)在平面PBC內，作BE⊥PC，E為垂足，連結DE，得PC⊥平面BED，從而DE⊥PC，即∠BED是二面角B－PC－D的平面角．在Rt△PAB中，由PA=AB=a∵ PA⊥平面ABCD，BC⊥AB∴ BC⊥PB(三垂線定理)在Rt△PBC中，在△BDE中，根據餘弦定理，得∴ ∠BED=120°即二面角B－PC－D的大小為120°．(2)過P作PQ ∥AB，則PQ平面PAB，∵ AB∥CD ∴ PQ∥CD，PQ平面PCD∴ 平面PAB∩平面PCD於PQ∵ PA⊥AB，AB∥PQ ∴ PA⊥PQ∵ PA⊥平面ABCD，CD⊥AD∴ CD⊥PD(三垂線定理的逆定理)∵ PQ∥CD ∴ PD⊥PQ所以∠APD是平面PAB和平面PCD所成的二面角的平面角．∵ PA=AB=AD，∴∠APD=45°即平面PAB和平面PCD所成的二面角為45°.評註 在求無棱二面角的大小時有時須作出稜線后再找平面角．

銳角三角形外心在三角形內部。

直角三角形外心在三角形斜邊中點。

鈍角三角形外心在三角形外。

有外心的圖形，一定有外接圓(各邊中垂線的交點，叫做外心）

外接圓圓心到三角形各個頂點的線段長度相等

過三角形的三個頂點的圓叫做三角形的外接圓，其圓心叫做三角形的外心。在三角形中，三角形的外心不一定在三角形內部，可能在三角形外部（如鈍角三角形）也可能在三角形邊上（如直角三角形）。

過不在同一直線上的三點可作一個圓（且只有一個圓）。