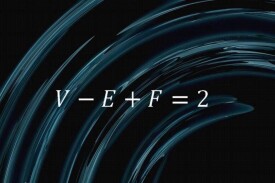多面體歐拉定理

式中V表示多面體的頂點數，E表示棱數，F表示面數。定理一證。

分析：以四面體ABCD為例。

將它的一個面BCD去掉，再使它變為平面圖形，四面體的頂點數V、棱數E與剩下的面數F1變形后都沒有變（這裡F1=F-1）。因此，要研究V、E和F的關係，只要去掉一個面，將它變形為平面圖形即可。

只需平面圖形證明：V+F1-E=1。

（1）去掉一條棱，就減少一個面，V+F1-E的值不變。例如去掉BC，就減少一個面ABC。同理，去掉CD、BD，也就各減少一個面ACD、ABD，由於V、F1-E的值都不變，因此V+F1-E的值不變。

（2）再從剩下的樹枝形中，去掉一條棱，就減少一個頂點，V+F1-E的值不變。例如去掉CA，就減少一個頂點C。同理去AD就減少一個頂點D，最後剩下AB。

在以上變化過程中，V+F1-E的值不變。

V+F1-E=2-0-1=1。

所以V+F-E=V+F1-E+1=2。

對任意的簡單多面體，運用這樣的方法，都是只剩下一條線段。公式對任意簡單多面體都是正確的。

（1）數學規律：公式描述了簡單多面體中頂點數、面數、棱數之間特有的規律。

（2）思想方法創新訓練：在定理的發現及證明過程中，在觀念上，假設它的表面是橡皮薄膜製成的，可隨意拉伸；在方法上將底面剪掉，然後其餘各面拉開鋪平，化為平面圖形（立體圖→平面圖）。

（3）引入拓撲新學科：“拉開圖”與以前的展開圖是不同的，從立體圖到拉開圖，各面的形狀，以及長度、距離、面積、全等等與度量有關的量發生了變化，而頂點數，面數，棱數等不變。

事實上，定理在引導大家進入一個新幾何學領域：拓撲學。我們用一種可隨意變形但不得撕破或粘連的材料（如橡皮波）做成的圖形，拓撲學就是研究圖形在這種變形過程中的不變的性質。

（4）給出多面體分類方法：

在歐拉公式中，令f(p)=V+F-E，f(p)叫做歐拉示性數。定理告訴我們，簡單多面體的歐拉示性數f(p)=2。

除簡單多面體外，還有不是簡單多面體的多面體。例如，將長方體挖去一個洞，連結底面相應頂點得到的多面體。它的表面不能經過連續變形變為一個球面，而能變為一個環面，它的歐拉示性數為f(p)=16+16-32=0，所以帶一個洞的多面體的歐拉示性數等於零。

多面體，設頂點數V，面數F，棱數E。剪掉一個面，將其餘的面拉平，使它變為平面圖形，我們在求所有面的內角總和Σα一方面，在利用面求內角總和。設有F個面，各面的邊數分別為n1,n2，…，nF，各面的內角總和為：Σα=[(n1-2)·180°+(n2-2)·180°+…+(nF-2)·180°]

=(n1+n2+…+nF-2F)·180°

=(2E-2F)·180°=(E-F)·360°（1）

另一方面，利用頂點來求內角總和。

設剪去的一個面為n邊形，其內角和為(n-2)·180°，則所有V個頂點中，有n個頂點在邊上，V-n個頂點在中間。中間V-n個頂點處的內角和為(V-n)·360°，邊上的n個頂點處的內角和(n-2)·180°。所以，多面體所有各面的內角和為：

Σα=(V-n)·360°+(n-2)·180°+(n-2)·180°=（V-2）·360°.（2）

由（1）（2）得

(E-F)·360°=（V-2）·360°

所以V+F-E=2.