共找到3條詞條名為多面體的結果 展開
多面體
數學概念
多面體是指四個或四個以上多邊形所圍成的立體。它有三個相關的定義,在傳統意義上,它是一個三維的多胞形,而在更新的意義上它是任何維度的多胞形的有界或無界推廣。將後者進一步一般化,就得到拓撲多面體。
由若干個平面多邊形圍成的幾何體叫做多面體。圍成多面體的多邊形叫做多面體的面。兩個面的公共邊叫做多面體的棱。若干條棱的公共頂點叫做多面體的頂點。把多面體的任何一個面伸展,如果其他各面都在這個平面的同側,就稱這個多面體為凸多面體。多面體至少有4個面。多面體依面數分別叫做四面體、五面體、六面體等等。把一個多面體的面數記作F,頂點數記作V,棱數記作E,則F、E、V滿足如下關係:F+V=E+2。
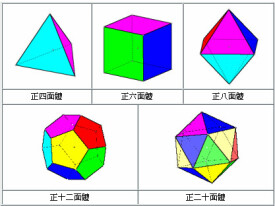
這就是關於多面體面數、頂點數和棱數的歐拉定理,每個面都是全等的正多邊形的多面體叫做正多面體。每面都是正三角形的正多面體有正四面體、正八面體和正二十面體。每面都是正方形的多面體只有正六面體即正方體,每面都是正五邊形的只有正十二面體。由歐拉定理可知一共只有這5種正多面體。
有兩個面互相平行,其餘各面都是四邊形,並且每相鄰兩個四邊形的公共邊都互相平行的多面體叫做稜柱(如圖1)。兩個互相平行的面叫稜柱的底面,其餘各面叫稜柱的側面,兩個側面的公共邊叫做稜柱的側棱,側面與底面的公共頂點叫做稜柱的頂點。不在同一個面上的兩個頂點的連線叫稜柱的對角線。兩個底面間的距離叫做稜柱的高。側棱不垂直於底面的稜柱叫做斜稜柱。側棱垂直於底面的稜柱叫做直稜柱。底面是正多邊形的直稜柱叫做正稜柱。底面是三角形、四邊形、五邊形……的稜柱分別叫做三稜柱、四稜柱、五稜柱……。容易看出稜柱的側棱的長都相等,側面都是平行四邊形。兩個底面與平行於底面的截面是全等的多邊形。過不相鄰的兩條側棱的截面是平行四邊形。直稜柱的側棱長與高相等,側面及經過不相鄰的兩條側棱的截面都是矩形。底面是平行四邊形的四稜柱叫做平行六面體。底面是矩形的直平行六面體叫做長方體。棱長都相等的長方體叫做正方體。易見長方體的一條對角線的長的平方等於一個頂點上3條棱長的平方和,稱垂直於側棱並與每條側棱都相交的截面為稜柱的直截面。斜稜柱的側面積等於它的直截面的周長與側棱長的乘積。直稜柱的底面是直截面,因此直稜柱的側面積等於它的底面的周長與一條側棱長的乘積。稜柱的體積等於它的底面積與高的乘積。
面與面之間僅在棱處有公共點,且沒有任何兩個面在同一平面上。一個多面體至少有四個面。
通常情況下,只有當多面體的所有面均為平面且單聯通,並且其所包圍的內部空間單聯通時,才為經典多面體
注意:各面都是平面的立體圖形稱為多面體。像圓錐、圓台因為有的面是曲面,而不被稱為“多面體”。圓錐、圓柱、圓台統稱為旋轉體。立體圖形的各個面都是平的面,這樣的立體圖形稱為多面體。
一個小竅門:從正六面體開始,每兩個正多面體的棱數相同,頂點數與面數正好相反,但只適用於一部分正多面體。
在經典意義上,一個多面體(polyhedron)(英語詞來自希臘語πολυεδρον,poly-,就是詞根πολυς,代表"多",+-edron,來自εδρον,代表"基底","座",或者"面")是一個三維形體,它由有限個多邊形面組成,每個面都是某個平面的一部分,面相交於邊,每條邊是直線段,而邊交於點,稱為頂點。立方體,稜錐和稜柱都是多面體的例子。多面體包住三維空間的一塊有界體積;有時內部的體也視為多面體的一部分。一個多面體是多邊形的三維對應。多邊形,多面體和更高維的對應物的一般術語是多胞體。
正多面體:所謂正多面體,是指多面體的各個面都是全等的正多邊形,並且各個多面角都是全等的多面角。例如,正四面體(即正稜錐體)的四個面都是全等的三角形,每個頂點有一個三面角,共有三個三面角,可以完全重合,也就是說它們是全等的。
正多面體的種數很少。多面體可以有無數,但正多面體只有正四面體、正六面體、正八面體、正十二面體、正二十面體五種。其中面數最少的是正四面體,面數最多的是正二十面體。有些化學元素的結晶體呈正多面體的形狀,如食鹽的結晶體是正六面體,明礬的結晶體是正八面體。
古希臘的畢達哥拉斯學派曾對五種小多面體作過專門研究,並將研究成果拿到柏拉頓學校教授。故而,西方數學界也將這五種正多面體稱為柏拉頓立體。
| 類型 | 面數 | 棱數 | 頂點數 | 每面邊數 | 每頂點棱數 |
| 正4面體 | 4 | 6 | 4 | 3 | 3 |
| 正6面體 | 6 | 12 | 8 | 4 | 3 |
| 正8面體 | 8 | 12 | 6 | 3 | 4 |
| 正12面體 | 12 | 30 | 20 | 5 | 3 |
| 正20面體 | 20 | 30 | 12 | 3 | 5 |
正多面體,或稱柏拉圖立體,指各面都是全等的正多邊形且每一個頂點所接的面數都是一樣的凸多面體。因此對於每兩個頂點來說都有一個等距的映射將其中一點映射到另一點。
命名由來
正多面體的別稱柏拉圖立體是因柏拉圖而命名的。柏拉圖的朋友特埃特圖斯告訴柏拉圖這些立體,柏拉圖便將這些立體寫在《提瑪友斯》內。正多面體的作法收錄《幾何原本》的第13卷。在命題13描述正四面體的作法,命題14就是正八面體,命題15為立方體,命題16是正二十面體,命題17是正十二面體。
判斷依據
判斷正多面體的依據有三條:
(1)正多面體的面由正多邊形構成
(2)正多面體的各個頂角相等
(3)正多面體的各條棱長都相等
這三個條件都必須同時滿足,否則就不是正多面體,比如五角十二面體,雖然和正十二面體一樣是由十二個五角形圍成的,但是由於它的各個頂角並不相等因此不是正多面體。
正多邊形都是軸對稱圖形,正偶數邊形既是軸對稱圖形又是中心對稱圖形如果n是偶數,則這些軸線中有一半經過相對的頂點,另外一半經過相對邊的中點。如果n是奇數,則所有的軸線都是經過一個頂點以及其相對邊的中心。例如:正多邊形的周長與它的外接圓的直徑的比值,與直徑長短無關。古代數學家正是利用這一性質,逐次倍增正多邊形的邊數,使正多邊形的周長趨近它的外接圓的周長,從而求得了圓周率的近似值。
多面體要素
多面體要素是一種可存儲面集合的GIS對象,能夠在資料庫中將3D對象的邊界表示為單個行。面可存儲表示要素組成部分的紋理、顏色、透明度和幾何信息。面中存儲的幾何信息可以是三角形、三角扇、三角條帶或環。
所有多面體都將z值作為用於構建面的坐標系的一部分而存儲。儘管可以使用數字要素屬性建立多面體的基礎z值模型,但此選項可能不支持使用嵌入式z值時可用的相同分析和交互選項。
有些多面體要素被視為已閉合,這表示它們正確定義了體積。閉合的多面體可用於其他分析工具,如3D聯合和3D相交。要將多面體視為已閉合,必須以正確方式構造該多面體。要素必須代表一個相異的體積。構成該體積的面必須具有與其坐標相同的逆時針方向並參與定義體積的外殼。這些面不得彼此相交,並且殼中不得存在間距或空白空間。可以使用是否為閉合地理處理工具來驗證多面體是否已正確閉合。
多面體要素的示例包括帶紋理的建築物、燈柱、樹、子表面地層、地下建築物或某種類型的分析表面。
創建多面體要素類
要創建新的多面體要素類,只需在定義要素類的幾何時從類型下拉菜單中選擇“多面體要素”。
z值
Z值用於表示多面體要素的形狀和高程。它可以表示絕對高度或相對於地面的高度。對生成的3D要素類進行顯示和分析時,兩種方法均完全受支持。
應該在要素類所在的要素數據集(如果存在)或在要素類自身(如果沒有要素數據集)中定義要素類z值的單位和基準面。如果未定義單位,ArcGIS將假定z的單位與x,y的單位匹配。此假定可能會帶來問題,尤其當x,y的單位是地理單位(緯度-經度)時。
創建多面體要素
使用地理處理工具將現有3D模型導入到ArcGIS中可創建多面體要素。3D圖層到要素類地理處理工具會將通過各種模型格式(如SketchUp、OpenFlight、3ds或COLLADA)符號化的點轉換為多面體要素類。導入3D文件地理處理工具也可執行相同操作,但會提供更多導入格式選項(如VRML)。此外,也可使用ArcObjects以程序的方式來構造多面體要素。