三角函數公式
數學中屬於初等函數中的超越函數的函數
三角函數是數學中屬於初等函數中的超越函數的函數。它們的本質是任何角的集合與一個比值的集合的變數之間的映射。通常的三角函數是在平面直角坐標系中定義的。其定義域為整個實數域。另一種定義是在直角三角形中,但並不完全。現代數學把它們描述成無窮數列的極限和微分方程的解,將其定義擴展到複數系。
三角函數公式看似很多、很複雜,但只要掌握了三角函數的本質及內部規律,就會發現三角函數各個公式之間有強大的聯繫。而掌握三角函數的內部規律及本質也是學好三角函數的關鍵所在。
| 銳角三角函數 | 任意角三角函數 | |
|---|---|---|
| 圖形 | 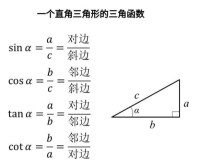 三角函數公式 | 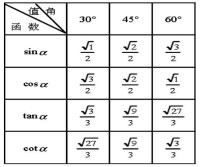 三角函數公式 |
| 正弦(sin) | sinA=a/c | sinθ=y/r |
| 餘弦(cos) | cosA=b/c | cosθ=x/r |
| 正切(tan或tg) | tanθ=a/b | tanθ=y/x |
| 餘切(cot或ctg) | cotA=b/a | cotθ=x/y |
| 正割(sec) | secA=c/b | secθ=r/x |
| 餘割(csc) | cscA=c/a | cscθ=r/y |
表格參考資料來源:現代漢語詞典.
倒數關係:①tanαcotα=1;②sinαcscα=1;③cosαsecα=1
商數關係:①tanα=sinα/cosα;②cotα=cosα/sinα.
平方關係:①sin^2α+cos^2α=1②1+tan^2α=sec^2α;③1+cot^2α=csc^2α
公式一:設α為任意角,終邊相同的角的同一三角函數的值相等:
公式二:為α任意角,π+α與的三角函數值之間的關係:
sin(2kπ+α)=sinα(k為整數)
cos(α+k*2π)=cosα(k為整數)
tan(α+k*2π)=tanα(k為整數)
cot(α+k*2π)=cotα(k為整數)
公式三:任意α角與-α的三角函數值之間的關係:
sin(2kπ-α)=-sinα
cos(2kπ-α)=cosα
tan(2kπ-α)=-tanα
cot(2kπ-α)=-cotα
公式四:利用公式二和公式三可以得到π-α與α的三角函數值之間的關係:
sin[(2k+1)π-α]=sinα
cos[(2k+1)π-α]=-cosα
tan[(2k+1)π-α]=-tanα
cot[(2k+1)π-α]=-cotα
公式五:利用公式一和公式三可以得到2π-α與α的三角函數值之間的關係:
sin(2kπ-α)=-sinα
cos(2kπ-α)=cosα
tan(2kπ-α)=-tanα
cot(2kπ-α)=-cotα
公式六:π/2±α與α的三角函數值之間的關係:
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
誘導公式口訣“奇變偶不變,符號看象限”意義:
k×π/2±a(k∈z)的三角函數值
(1)當k為偶數時,等於α的同名三角函數值,前面加上一個把α看作銳角時原三角函數值的符號;
(2)當k為奇數時,等於α的異名三角函數值,前面加上一個把α看作銳角時原三角函數值的符號。
記憶方法一:奇變偶不變,符號看象限:
記憶方法二:無論α是多大的角,都將α看成銳角.
以誘導公式二為例:
若將α看成銳角(終邊在第一象限),則π+α是第三象限的角(終邊在第三象限),正弦函數的函數值在第三象限是負值,餘弦函數的函數值在第三象限是負值,正切函數的函數值在第三象限是正值。這樣,就得到了誘導公式二
以誘導公式四為例:
若將α看成銳角(終邊在第一象限),則π-α是第二象限的角(終邊在第二象限),正弦函數的三角函數值在第二象限是正值,餘弦函數的三角函數值在第二象限是負值,正切函數的三角函數值在第二象限是負值。這樣,就得到了誘導公式四。
誘導公式的應用:
運用誘導公式轉化三角函數的一般步驟:
特別提醒:三角函數化簡與求值時需要的知識儲備:①熟記特殊角的三角函數值;②注意誘導公式的靈活運用;③三角函數化簡的要求是項數要最少,次數要最低,函數名最少,分母能最簡,易求值最好。
二角和差公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
cot(α+β)=cotαcotβ-1/cotβ+cotα
cot(α-β)=cotαcotβ+1/cotβ-cotα
證明如圖:負號的情況只需要用-β代替β即可.cot(α+β)推導只需把角α對邊設為1,過程與tan(α+β)相同.

三角函數公式
三角和公式:
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ
cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ
tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanα·tanγ)
口訣:正加正,正在前,余加余,余並肩,正減正,余在前,余減余,負正弦.
sinx+siny=2sin((x+y)/2)*cos((x-y)/2)
sinx-siny=2cos((x+y)/2)*sin((x-y)/2)
cosx+cosy=2cos((x+y)/2)*cos((x-y)/2)
cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2)
sina*cosb=(sin(a+b)+sin(a-b))/2
cosa*sinb=(sin(a+b)-sin(a-b))/2
cosa*cosb=(cos(a+b)+cos(a-b))/2
sina*sinb=-(cos(a+b)-cos(a-b))/2
二倍角公式:sin2αbai=2sinαcosα
tan2αdu=2tanα/(1-tan^zhi2(α))
cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
三倍角公式sin3α=3sinα-4sin^3 α=4sinα·sin(π/3+α)sin(π/3-α)
cos3α=4cos^3 α-3cosα=4cosα·cos(π/3+α)cos(π/3-α)
tan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)=tan a · tan(π/3+a)· tan(π/3-a)
證明:
sin3a
=sin(a+2a)
=sin2a·cosa+cos2a·sina
=2sina(1-sina)+(1-2sina)sina
=3sina-4sina
cos3a
=cos(2a+a)
=cos2acosa-sin2asina
=(2cosa-1)cosa-2(1-cosa)cosa
=4cosa-3cosa
sin3a
=3sina-4sina
=4sina(3/4-sina)
=4sina(sin60°+sina)(sin60°-sina)
=4sina×2sin[(60+a)/2]cos[(60°-a)/2]×2sin[(60°-a)/2]cos[60°+a)/2]
=4sinasin(60°+a)sin(60°-a)
cos3a
=4cosa-3cosa
=4cosa(cosa-3/4)
=4cosa(cosa-cos30°)(cosa+cos30°)
=4cosa×2cos[(a+30°)/2]cos[(a-30°)/2]×{-2sin[(a+30°)/2]sin[(a-30°)/2]}
=-4cosasin(a+30°)sin(a-30°)
=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]
=-4cosacos(60°-a)[-cos(60°+a)]
=4cosacos(60°-a)cos(60°+a)
上述兩式相比可得:
tan3a=tana·tan(60°-a)·tan(60°+a)
四倍角公式
sin4a=-4×[cosa·sina·(2×sina-1)]
cos4a=8cosa-8cosa+1
tan4a=(4tana-4tana)/(1-6tana+tana)
五倍角公式
sin5A=16sinA^5-20sinA^3+5sinA
cos5A=16cosA^5-20cosA^3+5cosA
tan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)
n倍角公式
根據棣莫弗定理,(cosθ+ i sinθ)^n = cos(nθ)+ i sin(nθ)
為方便描述,令sinθ=s,cosθ=c
考慮n為正整數的情形:
cos(nθ)+ i sin(nθ) = (c+ i s)^n = C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n- 4)*(i s)^4 + ... …+C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... …=>;比較兩邊的實部與虛部
實部:cos(nθ)=C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... …i*
虛部:i*sin(nθ)=C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... …
對所有的自然數n:
⒈cos(nθ):
公式中出現的s都是偶次方,而s^2=1-c^2(平方關係),因此全部都可以改成以c(也就是cosθ)表示。
⒉sin(nθ):
⑴當n是奇數時:公式中出現的c都是偶次方,而c^2=1-s^2(平方關係),因此全部都可以改成以s(也 就是sinθ)表示。
⑵當n是偶數時:公式中出現的c都是奇次方,而c^2=1-s^2(平方關係),因此即使再怎麼換成s,都至少會剩c(也就是 cosθ)的一次方無法消掉。
sin²(α/2)=(1-cosα)/2
cos²α/2)=(1+cosα)/2
tan²(α/2)=(1-cosα)/(1+cosα)
sin(α/2)=±[(1-cosα)/2]^(1/2)(正負由α/2所在象限決定)
sinα=2tan(α/2)/1+tan^2(α/2)
cosα=(1-tan^(α/2))/(1+tan^(α/2))
tanα=2tan^(α/2)/(1-tan^(α/2))
asinx+bcosx=Sqrt(a²+b²)sin(x+φ),tanφ=b/a.
詳見詞條:正弦定理
在任意△ABC中,角A、B、C所對的邊長分別為a、b、c,三角形外接圓的半徑為R.則有:a/sinA=b/sinB=c/sinC=2R
正弦定理變形可得:s=1/2absinC=1/2acsinB=1/2bcsinA=abc/4R
a=2RsinA,b=2RsinB,c=2RsinC
a:b:c=sinA:sinB:sinC
詳見詞條:餘弦定理
對於如圖所示的邊長為a、b、c而相應角為α、β、γ的△ABC,有:
a^2=b^2+c^2-2bc*cosA
b^2=c^2+a^2-2ac*cosB
c^2=a^2+b^2-2ab*cosC
也可表示為:cosA=b^2+c^2-a^2/2bc
cosB=c^2+a^2-b^2/2ca
cosC=a^2+b^2-c^2/2ab
sin²α=[1-cos(2α)]/2
cos²α=[1+cos(2α)]/2
tan²α=[1-cos(2α)]/[1+cos(2α)]
c0+c1x+c2x+...+cnx+...=∑cnx (n=0..∞)
c0+c1(x-a)+c2(x-a)+...+cn(x-a)+...=∑cn(x-a) (n=0..∞)
它們的各項都是正整數冪的冪函數, 其中c0,c1,c2,...cn...及a都是常數,這種級數稱為冪級數。
泰勒展開式又叫冪級數展開法
實用冪級數:
e= 1+x+x/2!+x/3!+…+x/n!+…,x∈R
ln(1+x)=x-x2/2+x3/3-…+(-1)x/k, x∈(-1,1)
sin x = x-x/3!+x/5!-…+(-1)x/(2k-1)!+…, x∈R
cos x = 1-x/2!+x/4!-…+(-1)x/(2k)!+…, x∈R
arcsin x = x + x/(2×3) + (1×3)x/(2×4×5) + (1×3×5)x/(2×4×6×7)…+(2k+1)!!×x/(2k!!×(2k+1))+…, x∈(-1,1)(!!表示雙階乘)
arccos x = π/2 -[x + x/(2×3) + (1×3)x/(2×4×5) + (1×3×5)x/(2×4×6×7)……], x∈(-1,1)
arctan x = x - x/3 + x/5 -…, x∈(-∞,1)
sinh x = x+x/3!+x/5!+…+x/(2k-1)!+…, x∈R
cosh x = 1+x/2!+x/4!+…+x/(2k)!+…, x∈R
arcsinh x =x - x/(2×3) + (1×3)x/(2×4×5) -(1×3×5)x/(2×4×6×7)…, x∈(-1,1)
arctanh x = x + x/3 + x/5 + …, x∈(-1,1)
在解初等三角函數時,只需記住公式便可輕鬆作答,在競賽中,往往會用到與圖像結合的方法求三角函數值、三角函數不等式、面積等等。
tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)
傅里葉級數又稱三角級數
f(x)=a0/2+∑(n=0..∞) (ancosnx+bnsinnx)
a0=1/π∫(π..-π) (f(x))dx
an=1/π∫(π..-π) (f(x)cosnx)dx
bn=1/π∫(π..-π) (f(x)sinnx)dx
