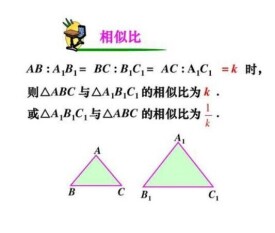
相似比

1、相似三角形的定義：對應角相等，對應邊成比例的三角形，叫做相似三角形。2、定理：平行於三角形的一邊的直線和和其他兩邊（或兩邊的延長線）相交，所構成的三角形與原三角形相似。3、相似三角形的傳遞性：如果△ABC ∽ △A₁B₁C₁，△A1B1C1 ∽ △A₂B₂C₂，那麼△ABC ∽ △A₂B₂C₂。

​

三角形相似比性質

1.相似三角形的一切對應線段(對應高線、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等於相似比;

2.相似三角形周長的比等於相似比;

3.相似三角形面積的比等於相似比的平方;

4.相似三角形內切圓、外接圓直徑比和周長比都和相似比相同，內切圓、外接圓面積比是相似比的平方。

（1）根據定義：對應角相等，對應邊成比例的三角形相似。（2）根據平行線：平行於三角形一邊的直線和其他兩邊（或兩邊的延長線）相交，所構成的三角形與原三角形相似。（3）判定定理1：兩角對應相等的兩個三角形相似。（4）判定定理2：兩邊對應成比例且夾角相等，兩三角形相似。

（5）判定定理3：三邊對應成比例，兩三角形相似。（6）直角三角形被斜邊上的高分成的兩個直角三角形和原三角形相似。