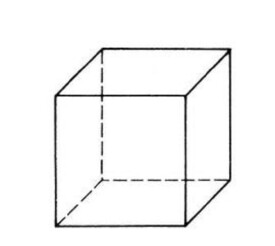
六面體
有六個面的空間形體
六面體就是有六個面的空間形體，共分為正六面體（也叫正方體）、平行六面體、不規則六面體三類。棱長相等的長方體叫做正方體，又稱“立方體”、“正六面體”。底面是平行四邊形的四稜柱叫做平行六面體。形狀不規則的稱為不規則六面體。
六面體可能有0條、1條、2條、4條對角線，但沒有3條對角線，也沒有5條或更多的對角線。
所謂的六面體，就是有六個面的空間形體。
第一類是：正六面體，也叫正方體。
第二類是：平行六面體。
第三類是：不規則六面體。
定義：棱長相等的長方體叫做正方體，又稱“立方體”、“正六面體”。
特徵是：
〔1〕有6個面，每個面面積相等，形狀完全相同；
〔2〕有8個頂點；
〔3〕有12條棱，每條棱長度相等。
因為6的面全部相等，所以
設一個正方體的棱長為a，則它的表面積。
；設一個正方體的棱長為a，則它的體積為：。
定義：底面是平行四邊形的四稜柱叫做平行六面體。
特徵是：
①平行六面體的任何一個面都可以作為底面；
②平行六面體的對角線交於一點，並且在交點處互相平分；
③平行六面體的四條對角線的平方和等於各棱的平方和；
④長方體的一條對角線的平方等於一個頂點上三條棱長的平方和。
若平行六面體的四條對角線長為定值且相交於點O，以O為球心的球半徑為r，則該球面上任意一點與該平行六面體的各頂點連線的距離平方和為定值。
直平行六面體：側棱與底面垂直的平行六面體叫直平行六面體。也可以說底面為平行四邊形的直四稜柱叫直平行六面體。
要回答這個問題，必須弄清六面體有多少種構造方式。
引理：若一個多面體p有一個面是k邊形，則p至少有個面。
證明：由於k邊形的每條邊恰屬於p的兩個面，除去這個k邊形所在的面，k條邊還屬於k個面，故p至少還有k個面，因此，p至少有個面。
由引理可知，六面體的各個面只可能是三角形、四邊形或五邊形。約定六面體的三角形數、四邊形數、五邊形數用數組(x，y，z)表示，用V、F、E分別表示六面體的頂點數、面數和棱數。如果有m條棱交於一點，就稱這個頂點為m棱頂點。
由於，由歐拉足理，有
由已知，有：
因為多面體的棱數等於各面邊數之和的一半，故有
再由，聯立上述各式得：
。
故可分為九種情況，
（1）、（2）、（3）、（4）
（5）、（6）、（7）、（8）
（9）
其中，（3）（4）對應的六面體不存在，因此可得到六面體可能有0條、1條、2條、4條對角線，但沒有3條對角線，也沒有5條或更多的對角線。
基本信息
- 中文名
- 六面體
- 外文名
- hexahedron
- 術語類別
- 數學術語
- 定義
- 六個面的空間形體
- 學科
- 數理科學
- 正方體
- 棱長相等的長方體