共找到2條詞條名為六子棋的結果 展開
- 中國民間版圖遊戲
- 同名遊戲
六子棋
中國民間版圖遊戲
六子棋是流傳於中國民間的一類版圖遊戲。是一種雙人對弈搏殺的一種遊戲，交戰雙方棋子數均為六顆，故稱六子棋。六子棋的棋盤為3乘以3的方格。棋子可信手拿來，只要互相區分即可。
六子棋，又名連六棋，為改良自五子棋一般規則及連珠棋規中“先手必勝”之不合理情況及國際棋規中之繁複規則。發明人為台灣交通大學資訊工程系教授吳毅成。
，般六棋雙默況。遊戲棋圍困棋顆棋，判輸棋。般況玩。
規則五棋非似，除黑顆，黑雙輪流各，連六獲勝。
題，棋盤，甚限亦。般玩言，采圍棋九棋盤即。
對專業棋士而言，採用五十九路棋盤。專業棋士可用電腦玩五十九路棋盤；若不用電腦玩的話，也可以拿3×3個圍棋棋盤合併起來玩。由於棋盤接合的線也算一路，這9個棋盤共形成五十九路的大棋盤。當然，在實際對局時，應先用一個圍棋的十九路棋盤開始；當下超過棋盤時，才拿新的棋盤合併上去。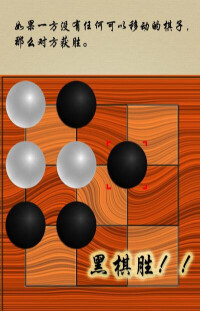
六子棋
槍斃，行棋一方若將兩顆棋子移至一起，且一頭挨著對方的一顆棋時，則可吃對方該子（稱為槍斃）。
六子棋
挑子，行棋一方一個棋子插入對方的兩個棋子中間時，則可吃對方該兩個棋子（稱為挑子）。
原則上，許多複雜的遊戲如圍棋及象棋等，也都無法宣稱絕對公平。因此對公平性，只能先從幾個角度來論證。
對六子棋來說，每當一方下出一步（兩子）時，該方一定比對方多出一顆子。這很自然地使得六子棋具有相當的公平性，不會偏向某個玩家。與五子棋相比，明顯地是較為公平的遊戲。
目前發明者完成了一個六子棋程式。這個程式大都可以擊敗一般玩家。這裡先由電腦產生一千多種開局的樣式，然後讓電腦對電腦下。直到目前為止，還沒有發現，對某一方，特別有利。
另外，吳教授也證明了白方不能脫離戰場，否則黑方勝。這個理論迫使雙方必須從中心點開始纏鬥。若白方能成功脫離主戰場，下到他處，則此遊戲變成每人下兩顆子，而先的一方（這時變成白方）第一手下兩顆子，這明顯對白方有利。
當然，公平性需要更多實戰的經驗，及一段時間的驗證。
對六子棋而言，因為公平性不是問題，所以棋盤是可以任意地大，甚至是無限大亦可。以上述的十九路棋盤為例，所謂狀態空間（Statespace）複雜度可達10172，與圍棋相當。而博弈樹（Gametree）複雜度，亦可達：至10140，遠大於五子棋。
若用五十九路棋盤，則狀態空間複雜度大過圍棋，而博弈樹複雜度也不亞於圍棋。
另外值得一提的是五子棋的棋盤是15×15的原因是：GoroSakata及WataruIkawa兩位專家提到愈大的棋盤，愈增加黑方獲勝的機會，因此需要縮小棋盤大小。然而很矛盾的是小棋盤，複雜度自然變小，反而讓電腦更容易窮舉出五子棋的勝負。
2003年暑假的某一天，吳毅成教授與女兒下五子棋中，發展出這個玩法。
2004年初，吳教授的碩士班學生黃德彥參與這項研究，並作為個人的碩士論文。
2005年初，他們完成了第一個六子棋程式，與電腦對弈，這個程式大都可以擊敗他們。而他們也製造出各種開局的樣式（有1283種），讓電腦對電腦下。直到目前為止，還沒有發現，對某一方，特別有利。
2005年9月，他們整理這些研究結果成為論文並發表在第十一屆的國際電腦賽局發展研討會中。其中提出一些理論，證明白方不能脫離戰場，否則黑方勝。這個理論迫使雙方必須從中心點開始纏鬥。
2005年9月，群想網路科技完成第一個六子棋線上遊戲提供免費試玩。
2005年9月20-21日，六子棋發表到台灣各大媒體。
2005年，有興趣的相關人士，開始討論籌組六子棋協會，並開闢六子棋論壇。
2006年5月，在義大利杜林舉辦的第11屆奧林匹亞電腦競賽（11thComputerOlympiad），第一次加入六子棋項目。吳教授之六子棋程式NCTU6獲得金牌，可參考詳細結果。
2006年7月16日，在台灣新竹舉辦第一屆交通大學杯公開賽，可參考詳細結果。
2007年8月24日，曾獲得世界圍棋棋王的周俊勛，公開嘗試與NCTU6對弈，三戰皆敗北。
2007年8月26日，在台灣新竹舉辦第二屆交通大學杯公開賽。
2007年10月，第二屆中國機器博弈錦標賽中首次加入六子棋項目，東北大學棋天大聖程序奪冠。
在江西省寧都縣農村，一直流傳有“六子棋”這一棋類遊戲。由於筆者是從自己的祖母那裡學會該棋類，而筆者的祖母應當也是從他人那裡學會的該棋類。有近百年或以上歷史。
棋盤。棋盤與本文中所述棋盤一致。
棋子擺放比較自由。假設以一條平行於底線的橫線將棋盤對半而分，對戰雙方可以將自己所持的6子任意的擺放在己方半邊3個方格的8個頂點的任意6個頂點上。
吃子。設對戰雙方各持黑子與白子。以黑子吃掉白子為例，若黑子的行棋應當在棋盤上形成某條棋盤線上兩個黑子緊靠著頂著一個緊挨著某個黑子的白子，且同一條棋盤線上只有那兩個黑子和一個白子，那麼白子將被吃掉。若由於白子的行走造成的雙黑字頂一個白子，則不構成黑子吃白子的條件。反之，白子吃黑字亦然。
勝負。在某一方最後只剩一個棋子時，比賽結束，以剩下棋子較多的一方為勝。若最終，步入僵局，雙方都無法再吃對方棋子時，則以剩下棋子較多的一方為勝，若雙方棋子數量一樣，那麼視為平局。
舊時，農閑時，或是在人們在地里勞動停下來休息時，大家在地上畫方格為棋盤，拾碎石、折樹枝作為棋子，以對弈。
基本信息
- 中文名
- 六子棋
- 外文名
- Connect6
- 類型
- 雙人對弈搏殺
- 流傳於
- 中國民間
- 人數
- 雙人