顯著性檢驗

顯著性檢驗即用於實驗處理組與對照組或兩種不同處理的效應之間是否有差異，以及這種差異是否顯著的方法。

常把一個要檢驗的假設記作H0,稱為原假設（或零假設） (null hypothesis) ，與H0對立的假設記作H1，稱為備擇假設(alternative hypothesis) 。

⑴ 在原假設為真時，決定放棄原假設，稱為第一類錯誤，其出現的概率通常記作α；

⑵ 在原假設不真時，決定不放棄原假設，稱為第二類錯誤，其出現的概率通常記作β

(3)α+β 不一定等於1。

通常只限定犯第一類錯誤的最大概率α，不考慮犯第二類錯誤的概率β。這樣的假設 檢驗又稱為顯著性檢驗，概率α稱為顯著性水平。

最常用的α值為0.01、0.05、0.10等。一般情況下，根據研究的問題，如果放棄真假設損失大，為減少這類錯誤，α取值小些，反之，α取值大些。

為什麼要進行顯著性檢驗進行顯著性檢驗是為了消除第一類錯誤和第二類錯誤。通常情況下，α水平就是第一類錯誤。第一類錯誤是零假設為真卻被錯誤拒絕的概率。第二類錯誤()是零假設為誤卻被錯誤接受的概率或是研究假設為真卻被拒絕的概率。如果P值小於某個事先確定的水平，理論上則拒絕零假設，反之，如果P值大於某個事先確定的水平，理論上則不拒絕零假設。常用的顯著性水平是0.05，0.01和0.001。不同的水平各有優缺點。水平越小，判定顯著性的證據就越充分，但是不拒絕錯誤零假設的風險，犯第二類錯誤的可能性就越大，統計效力(就越低。選擇水平不可避免地要在第一類錯誤和第二類錯誤之間做出權衡。如果犯第一類錯誤造成的後果不嚴重，比如在試探性研究中，我們可以將α水平定得高一些，如0.05或0.1。如果研究樣本很小，為了提高統計效力，我們在某些研究中也不妨提高口水平。但是，如果犯第一類錯誤造成的後果很嚴重，比如我們要基於某項研究發現決定是否在全國推行某項教學改革，我們則需要將α水平定得低一些，如0.01或0.001。

顯著性檢驗的基本原理是提出“無效假設”和檢驗“無效假設”成立的機率（P）水平的選擇。所謂“無效假設”，就是當比較實驗處理組與對照組的結果時，假設兩組結果間差異不顯著，即實驗處理對結果沒有影響或無效。經統計學分析后，如發現兩組間差異是抽樣引起的，則“無效假設”成立，可認為這種差異為不顯著（即實驗處理無效）。若兩組間差異不是由抽樣引起的，則“無效假設”不成立，可認為這種差異是顯著的（即實驗處理有效）。

檢驗“無效假設”成立的機率水平一般定為5%，其含義是將同一實驗重複100次，兩者結果間的差異有5次以上是由抽樣誤差造成的，則“無效假設”成立，可認為兩組間的差異為不顯著，常記為。若兩者結果間的差異5次以下是由抽樣誤差造成的，則“無效假設”不成立，可認為兩組間的差異為顯著，常記為。如果，則認為兩組間的差異為非常顯著。

顯著性檢驗的基本思想可以用小概率原理來解釋。

1、小概率原理：小概率事件在一次試驗中是幾乎不可能發生的，假若在一次試驗中小概率事件事實上發生了。那隻能認為該事件不是來自我們假設的總體，也就是認為我們對總體所做的假設不正確。

2、觀察到的顯著水平：由樣本資料計算出來的檢驗統計量觀察值所截取的尾部面積。這個概率越小，反對原假設，認為觀察到的差異表明真實的差異存在的證據便越強，觀察到的差異便越加理由充分地表明真實差異存在。

3、檢驗所用的顯著水平：針對具體問題的具體特點，事先規定這個檢驗標準。

4、在檢驗的操作中，把觀察到的顯著性水平與作為檢驗標準的顯著水平標準比較，小於這個標準時，得到了拒絕原假設的證據，認為樣本數據表明了真實差異存在。大於這個標準時，拒絕原假設的證據不足，認為樣本數據不足以表明真實差異存在。

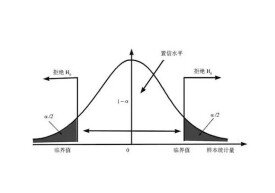
5、檢驗的操作可以用稍許簡便一點的作法：根據所提出的顯著水平查表得到相應的值，稱作臨界值，直接用檢驗統計量的觀察值與臨界值作比較，觀察值落在臨界值所劃定的尾部內，便拒絕原假設；觀察值落在臨界值所劃定的尾部之外，則認為拒絕原假設的證據不足。

顯著性檢驗的一般步驟或格式，如下：

1、提出虛無假設和備擇假設

H0：______

H1：______

同時，與備擇假設相應，指出所作檢驗為雙尾檢驗還是左單尾或右單尾檢驗。

2、構造檢驗統計量，收集樣本數據，計算檢驗統計量的樣本觀察值。

3、根據所提出的顯著水平，確定臨界值和拒絕域

4、計算檢驗統計量的值。

5、作出檢驗決策。

把檢驗統計量的樣本觀察值和臨界值比較，或者把觀察到的顯著水平與顯著水平標準比較；最後按檢驗規則作出檢驗決策。當樣本值落入拒絕域時，表述成:“拒絕原假設”，“顯著表明真實的差異存在”；當樣本值落入接受域時，表述成：“沒有充足的理由拒絕原假設”，“沒有充足的理由表明真實的差異存在”。另外，在表述結論之後應當註明所用的顯著水平。

適用於計量資料、正態分佈、方差具有齊性的兩組間小樣本比較。包括配對資料間、樣本與均數間、兩樣本均數間比較三種，三者的計算公式不能混淆。（處理時不用判斷分佈類型就可以使用t檢驗）

應用條件與t檢驗大致相同，但t′檢驗用於兩組間方差不齊時，t′檢驗的計算公式實際上是方差不齊時t檢驗的校正公式。

應用條件與t檢驗基本一致，只是當大樣本時用U檢驗，而小樣本時則用t檢驗，t檢驗可以代替U檢驗。

用於正態分佈、方差齊性的多組間計量比較。常見的有單因素分組的多樣本均數比較及雙因素分組的多個樣本均數的比較，方差分析首先是比較各組間總的差異，如總差異有顯著性，再進行組間的兩兩比較，組間比較用q檢驗或LST檢驗等。

是計數資料主要的顯著性檢驗方法。用於兩個或多個百分比(率)的比較。常見以下幾種情況：四格表資料、配對資料、多於2行乘以2列資料及組內分組X2檢驗。

用於計數資料。是當實驗組或對照組中出現概率為0或100%時，X2檢驗的一種特殊形式。屬於直接概率計演演算法。

非參數統計方法

符號檢驗、秩和檢驗和Ridit檢驗

三者均屬非參數統計方法，共同特點是簡便、快捷、實用。可用於各種非正態分佈的資料、未知分佈資料及半定量資料的分析。其主要缺點是容易丟失數據中包含的信息。所以凡是正態分佈或可通過數據轉換成正態分佈者盡量不用這些方法。

Hotelling檢驗

用於計量資料、正態分佈、兩組間多項指標的綜合差異顯著性檢驗。

在試驗、檢測的數據處理過程中，時常會出現兩種或者多種不同的試驗結果。對數據進行比較分析時，不能僅憑兩個結果的不同就作出結論，而是要進行統計學分析，對數據進行差異顯著性檢驗。顯著性檢驗就是事先對總體(隨機變數 )的參數或總體分佈形式作出一個假設，然後利用樣本信息來判 斷這個假設(原假設 )是否合理，即判斷總體的真實情況與原假設是否存在顯著差異。這時我們要做兩種檢驗，一種是檢驗數據是否是屬於母體內抽取的樣本，即檢驗總體參數與樣本統計量之間是否存在著顯著的差異；另一種是檢驗數據的統計 量是 否存在著顯著的差異。差異顯著性檢驗就是要判定造成差異的原因，即差異是由於誤差或偶然因素引起的或兩者確實本身存在著差異。

顯著性檢驗是針對我們對總體所作的假設做檢驗，其原理就是“小概率事件實際不可能性原理”來接受或否定假設。所謂“顯著”，就是指兩種或多種處理試驗結果之間，本身確實存在差異。如果是“不顯著”，就說明它們之間的差異是 由抽樣或偶然 的因素引起的，不是真正有實際差異存在。

在數理統計中一般以概率 (P)5%作為顯著評定標準，即在100次試驗中，由於偶然 因素造成差異的可能 性在5次 以上，其差異被認為是不顯著。如果兩者差異在概率為5%的範圍內，出現這樣概率的機會非常小而出現了，那麼我們就認為此差數具有 顯著差異程度。有時我們認為 5%太低，則可提高到1%作 為顯著評定標準，若兩者的差異在概率為1%的範圍內，那麼我們就認為這個差數具有極顯著的差異程度。