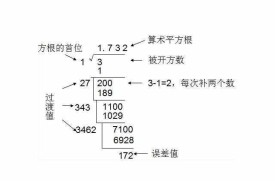
平方根計算

計算一個非負實數的平方根

功 能：一個非負實數的平方根

函數原型：在VC6.0中的math.h頭文件的函數原型為double sqrt(double);

說明：sqrt系Square Root Calculations（平方根計算），通過這種運算可以考驗CPU的浮點能力。

目錄
1程序例 2pascal 3gcc
4EXCEL函數 5Python函數 6C++

程序例

1
2
3
4
5
6
7
8
9
#include
#include
int main(void)
{
double x = 4.0,result;
result = sqrt(x); //result*result=x
printf("Thesquarerootof%fis%f\n",x,result);
return 0;
}
VC 2008後為重載函數，原型為 float sqrt (float),double sqrt (double),double long sqrt(double long)
注意沒有sqrt (int)，但是返回值可以為int
John Carmack's sqrt [C/C++]
Carmack的sqrt計算函數在批量計量時的耗時比系統庫函數還要少，優異的性能的根本原因就是那個令無數人膜拜的魔數0x5F3759DF。
1
2
3
4
5
6
7
8
9
10
11
12
static float CarmackSqrt (float x)
{
float xhalf = 0.5f * x;
int i = *(int*)&x; // get bits for floating VALUE 
i = 0x5f3759df - (i>>1); // gives initial guess y0
x = *(float*)&i; // convert bits BACK to float
x = x*(1.5f - xhalf*x*x); // Newton step, repeating increases accuracy
x = x*(1.5f - xhalf*x*x); // Newton step, repeating increases accuracy
x = x*(1.5f - xhalf*x*x); // Newton step, repeating increases accuracy
return (1 / x);
}

pascal

a := sqrt(sqr(x-x[j])+sqr(y-y[j]));
b := sqrt(sqr(x-x[k])+sqr(y-y[k]));
c := sqrt(sqr(x[j]-x[k])+sqr(y[j]-y[k]));

gcc

Linux 中使用gcc編譯器 需要加 -lm 作為鏈接，調用數學函數庫math.h
rand()函數是產生隨機數的一個隨機函數。函數包含在頭文件stdlib.h
例如：
1
2
3
4
5
6
7
8
9
10
11
12
#include
#include
//#include
void main()
{
double x;
double n=rand()%100;
printf("%lf\n",n);
x=sqrt(n);
printf("%lf\n",x);
}

EXCEL函數

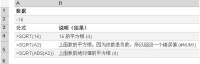
示例
示例
返回正平方根。
語法
SQRT（number）
Number 要計算平方根的數。
說明
如果參數 Number 為負值，函數 SQRT 返回錯誤值 #Num!。

Python函數

#!/usr/bin/env python
import math # This will import math module
print("math.sqrt(100) is:", math.sqrt(100))

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include 
//這裡的cmath等價於C的math.h
#include 
using namespace std;
int main()
{
double x, result;
cin>>x;
result=sqrt(x);
cout<
return 0;
}
//cmath等價於math.h,其就是using math.h的函數
//VC 2008後為重載函數，原型為 float sqrt (float),double sqrt (double),long double sqrt(long double)
1//注意沒有sqrt (int)，但是返回值可以為int

基本信息

中文名
平方根計算
外文名
sqrt
本質
程序函數
函數原型
double sqrt(double)
頭文件
math.h
應用
考驗CPU的浮點能力
功能
計算一個非負實數的平方根