希爾伯特變換
希爾伯特變換
在數學與信號處理的領域中,一個實值函數的希爾伯特變換(Hilbert transform)——在此標示為H——是將信號s(t)與1/(πt)做卷積,以得到s'(t)。因此,希爾伯特變換結果s'(t)可以被解讀為輸入是s(t)的線性時不變系統(linear time invariant system)的輸出,而此系統的脈衝響應為1/(πt)。這是一項有用的數學,用在描述一個以實數值載波做調製的信號之複數包絡(complex envelope),出現通訊理論中發揮著重要作用
希爾伯特變換是以著名數學家大衛·希爾伯特(David Hilbert)來命名。
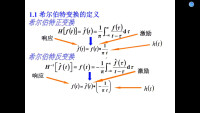
圖1
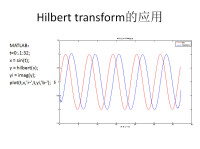
圖2
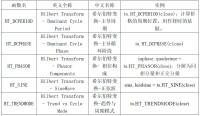
圖3
式中H(Ω)是h(t)的傅里葉變換,Ω表示角頻率,所以,已知H(Ω),則H(Ω)就被確定,反之也一樣。因此,如果給定系統函數的實部(虛部),就不能任意確定虛部(實部),否則就不能保證是因果系統。同理,一個穩定的最小相位系統,由於其對數幅度1og|H(Ω)|和對數相位arg〔H(Ω))〕之間互為希爾伯特變換,則該系統一定是因果系統。所以通常設計濾波器,當給定幅頻特性后,則其相頻特性就不能任意選擇。否則,不能保證系統是穩定和因果的。理想的希爾伯特變換器是非因果系統,採用數字信號處理技術,將信號適當延遲,比較容易實現一定頻帶範圍內,頻率特性是近似理想的。
希爾伯特變換定義如下:
其中

希爾伯特變換
希爾伯特變換之頻率響應由傅立葉變換給出:

Hw
常被稱作signum函數。既然:
希爾伯特實際上是一個使相位滯后pi/2的全通移相網路。
我們也注意到:H^2(\omega) = -1。因此將上面方程式乘上,可得到:
從中,可以看出反(逆)希爾伯特變換
在地震三瞬分析中希爾伯特變換存在的問題
通過希爾伯特變換,使得我們對簡訊號和複雜信號的瞬時參數的定義及計算成為可能,能夠實現真正意義上的瞬時信號的提取,因而希爾伯特變換在信號處理上具有十分重要的地位。然而,它也存在以下問題:
希爾伯特變換隻能近似應用於窄帶信號,即只適用 的信號,其中B(B為信號帶寬)。但實際應用中,存在許多非窄帶信號,希爾伯特變換對這些信號無能為力。即便是窄帶信號,如果不能完全滿足希爾伯特變換條件,也會使結果發生錯誤。而實際信號中由於雜訊的存在,會使很多原來滿足希爾伯特變換條件的信號無法完全滿足;
對於任意給定t時刻,通過希爾伯特變換運算后的結果只能存在一個頻率值,即只能處理任何時刻為單一頻率的信號;
對於一個非平穩的數據序列,希爾伯特變換得到的結果很大程度上失去了原有的物理意義。
首先,將實數信號變換成解析信號的結果就是,把一個一維的信號變成了二維複平面上的信號,複數的模和幅角代表了信號的幅度和相位。
這樣看來,似乎複數信號才是完整的,而實信號只是在複平面的實軸上的一個投影。我們知道,解析信號可以計算包絡(瞬時振幅)和瞬時相位。在上圖中可以看到,實際上我們計算的包絡就是黑色的線圍成的立體圖形的邊界在實部的投影,而計算這個邊的投影也很簡單,就是在複平面上的螺旋線中的每一個點的模值,也就是A(t) = sqrt(x^2(t) + Hilbert(x(t))^2),而瞬時相位就是虛部(Hilbert變換后的)和實部(原始信號)在某一時間點的比值的arctan,瞬時頻率就是它的導數。
