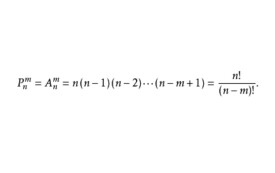排列

排列（permutation），數學的重要概念之一。有限集的子集按某種條件的序化法排成一列、排成一圈、不許重複或許重複等。從n個不同元素中每次取出m（1≤m≤n）個不同元素，排成一列，稱為從n個元素中取出m個元素的無重複排列或直線排列，簡稱排列。從n個不同元素中取出m個不同元素的所有不同排列的個數稱為排列種數或稱排列數，記為（或)，

註：當且僅當兩個排列的元素完全相同，且元素的排列順序也相同，則兩個排列相同。例如，abc與abd的元素不完全相同，它們是不同的排列；又如abc與acb，雖然元素完全相同，但元素的排列順序不同，它們也是不同的排列。

排列可分選排列與全排列兩種，在從n個不同元素取出m個不同元素的排列種，當m

一個從n個元素中取m個元素的排列可以看成這n個元素組成的集合A的一個m元有序子集，於是A的m元有序子集的個數為。

公式推導

---

排列公式是建立一個模型，從n個不相同元素中取出m個排成一列（有序），第一個位置可以有n個選擇，第二個位置可以有n-1個選擇（已經有1個放在前一個位置），則同理可知第三個位置可以有n-2個選擇，以此類推第m個位置可以有n-m+1個選擇，則排列數由階乘的定義可知上下合併可得

重複排列

---

重複排列(permutationwith repetiton)是一種特殊的排列。從n個不同元素中可重複地選取m個元素。按照一定的順序排成一列，稱作從n個元素中取m個元素的可重複排列。當且僅當所取的元素相同，且元素的排列順序也相同，則兩個排列相同。

由分步記數原理易知，從n個元素中取m個元素的可重複排列的不同排列數為。