標量
標量
標量(scalar),亦稱“無向量”。有些物理量,只具有數值大小,而沒有方向,部分有正負之分。物理學中,標量(或作純量)指在坐標變換下保持不變的物理量。用通俗的說法,標量是只有大小,沒有方向的量。
目錄
這些量之間的運算遵循一般的代數法則。這樣的量叫做“標量”。如質量、密度、溫度、功、能量、路程、速率、體積、時間、熱量、電阻等物理量。無論選取什麼坐標系,標量的數值恆保持不變。矢量和標量的乘積仍為矢量。矢量和矢量的乘積,可構成新的標量,也可構成新的矢量,構成標量的乘積叫標積。
矢量和標量的定義如下:(到大學物理中會詳細研究)
(1)定義或解釋:有些物理量,既要由數值大小(包括有關的單位),又要由方向才能完全確定。這些量之間的運算並不遵循一般的代數法則,而遵循特殊的運演演算法則。這樣的量叫做物理矢量。有些物理量,只具有數值大小(包括有關的單位),而不具有方向性。這些量之間的運算遵循一般的代數法則。這樣的量叫做物理標量。
(2)說明:①矢量之間的運算要遵循特殊的法則。矢量加法一般可用平行四邊形法則。由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的逆運算,一個矢量減去另一個矢量,等於加上那個矢量的負矢量。A-B=A+(-B)。矢量的乘法。矢量和標量的乘積仍為矢量。矢量和矢量的乘積,可以構成新的標量,矢量間這樣的乘積叫標積;也可構成新的矢量,矢量間這樣的乘積叫矢積。例如,物理學中,功、功率等的計算是採用兩個矢量的標積。W=F·S,P=F·v,物理學中,力矩、洛侖茲力等的計算是採用兩個矢量的矢積。M=r×F,F=qv×B。②物理定律的矢量表達跟坐標的選擇無關,矢量符號為表述物理定律提供了簡單明了的形式,且使這些定律的推導簡單化,因此矢量是學習物理學的有用工具。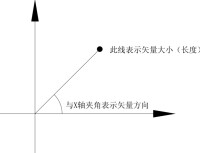

標量
