黎曼引理是在微積分學裡面一個比較重要的定理。內容如下:
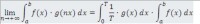
黎曼引理

黎曼引理
一元積分學中的黎曼引理: 若f(x)在[a,b]上可積, g(x)是以T為周期的
函數,在[0,T]上可積;則成立:不過較常用的還是另外一種表示,即:設函數f(x)在[a,b],上可積或者絕對可積,則成立:因為
正弦,餘弦函數在一個周期上積分都為零,所以後者可以看成前者的推論,但是要注意兩者的區別,後者有絕對可積,前者沒有。也正因為如此,後者相對而言,用處更大,在大學本科數學里,作為一條引理來運用,成為導出
傅里葉級數性質的強有力工具。